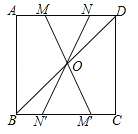
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
A.2对 B.3对 C.4对 D.5对
参考答案:
【答案】C.
【解析】
试题分析:∵四边形ABCD是正方形,∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,在△ABD和△BCD中,∵AB=BC,∠A=∠C,AD=CD,∴△ABD≌△BCD,∵AD∥BC,∴∠MDO=∠M′BO,在△MOD和△M′OB中,∵∠MDO=∠M'BO,∠MOD=∠M'OB,DM=BM',∴△MDO≌△M′BO,同理可证△NOD≌△N′OB,∴△MON≌△M′ON′,∴全等三角形一共有4对.故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察一列数a1=3,a2=9,a3=27,a4=81,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a
 = ,a
= ,a = ;(可用幂的形 式表示)
= ;(可用幂的形 式表示)(2)如果想要求1+2+22+2
 +…+2
+…+2 的值,
的值,可令S10=1+2+22+2
 +…+2
+…+2 ①
①将①式两边同乘以2,得2S10= ,②
由②式减去①式,得S10= .
(3)有一组数列,其中a1=1,a2=3,a3=9……an=3n-1,
请利用上述规律和方法计算a21+a22+a23+……a30的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
A.(0,﹣9)
B.(﹣6,﹣1)
C.(1,﹣2)
D.(1,﹣8) -
科目: 来源: 题型:
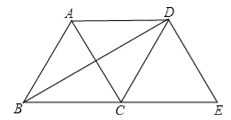
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点P(﹣1,4)向右平移2个单位长度后,再向下平移3个单位长度,得到点P1 , 则点P1的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为
 ;
;⑤当△ABP≌△ADN时,BP=
 .
.
相关试题

