【题目】如图,点E在△ABC外部,点D在边BC上,DE交AC于点F.若∠1=∠2=∠3,AC=AE,求证△ABC≌△ADE.

参考答案:
【答案】证明过程见解析
【解析】试题分析:要想证明△ABC≌△ADE,全等的条件,∵∠1=∠2=∠3,
∴∠2+∠DAC=∠1+∠DAC,∴∠BAC=∠DAE,又∵∠DFC=∠AFE,∠3=∠1,
∴在△ADE和△ABC中,由三角形的内角和定理得∠3+∠C+∠DFC=∠1+∠E+∠AFE,
∵∠DFC=∠AFE,∴∠C=∠E,又已知AD=AB,∴△ABC≌△ADE(AAS)
试题解析: (1)由三角形的内角和定理△AEF与△DCF中,
∵∠2=∠3,∠AFE=∠CFD, ∴∠C=∠E;∵∠1=∠2, ∠BAC=∠1+∠DAC,
∠DAE=∠2+∠DAC ∴∠BAC=∠DAE 又∵AC=AE, ∴△ABC≌△ADE(ASA)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某酒店为了吸引顾客,设立了一个可以自由转动的装盘,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,若指针正好对准八折、七折、五折区域,顾客就可以获得此待遇(转盘分成12等份).
(1)甲顾客消费了90元,是否可获得转动转盘的机会?
(2)乙顾客消费120元,获得打折待遇的概率是多少?他获得八折、七折待遇的概率分别是多少?
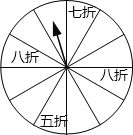
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠B 与∠C 的平分线交于点O, 过O 点作DE ∥BC,分别交AB、AC于D、E,若AB=5,AC=4,求△ADE 的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级某班组织班队活动,班委会准备买一些奖品。.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件。
【1】有多少种购买方案?请列举所有可能的结果;
【2】从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中,  ,点
,点 是直线
是直线 上一点(不与
上一点(不与 重合),以
重合),以 为一边在
为一边在 的右侧作
的右侧作 ,使
,使 ,连接
,连接 .
.(1)如图1,当点
 在线段
在线段 上,如果
上,如果 ,则
,则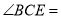 度;
度;(2)设
 ,
,  .
.①如图2,当点
 在线段
在线段 上移动,则
上移动,则 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;②当点
 在直线
在直线 上移动,则
上移动,则 之间有怎样的数量关系?请画出图形并直接写出相应的结论.
之间有怎样的数量关系?请画出图形并直接写出相应的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A.足球运动员射门一次,球射进球门B.随意翻开一本书,这页的页码是奇数
C.经过有交通信号灯的路口,遇到绿灯D.任意画一个三角形,其内角和是180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】冠状病毒有多种类型,新型冠状病毒也是其中的一种.冠状病毒的直径在60﹣220纳米之间,平均直径为100纳米左右(1纳米=10﹣9米).那么100纳米可用科学记数法表示为( )
A.100×10﹣9米B.100×109米C.1×10﹣7米D.1×107米
相关试题

