搜索
【题目】一组正方形按如图所示的方式放置，其中顶点B1在y轴上，顶点C1、E1、E2、C2、E3、E4、…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3∥…，则正方形A2018B2018C2018D2018的边长是_____．
参考答案：
【答案】（
）2017
【解析】分析：利用正方形的性质结合锐角三角函数关系得出正方形的边长，进而得出变化规律即可得出答案．
详解：∵正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3，∴D1E1=B2E2，D2E3=B3E4，∠D1C1E1=∠C2B2E2=∠C3B3E4=30°，∴D1E1=C1D1sin30°=
，则B2C2=
，同理可得：B3C3=
=（ ）2，故正方形AnBnCnDn的边长是：（ ）n﹣1，则正方形A2018B2018C2018D2018的边长为：（ ）2017．
故答案为：（ ）2017．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果三角形三边的长a、b、c满足
，那么我们就把这样的三角形叫做“匀称三角形”，如：三边长分别为1，1，1或3，5，7，…的三角形都是“匀称三角形”．（1）如图1，已知两条线段的长分别为a、c（a＜c）．用直尺和圆规作一个最短边、最长边的长分别为a、c的“匀称三角形”（不写作法，保留作图痕迹）；
（2）如图2，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作⊙O的切线交AB延长线于点E，交AC于点F，若
，判断△AEF是否为“匀称三角形”？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与X轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：
①4a﹣2b+c＜0；②2a﹣b＜0；③a+c＜1；④b2+8a＞4ac，
其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（ ）
①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上．
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
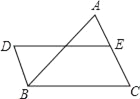
查看答案和解析>>【题目】如图，DB∥AC，且DB=
AC，E是AC的中点．（1）求证：BC=DE；
（2）连接AD、BE，若∠BAC=∠C，求证：四边形DBEA是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
（1）BD与CD有什么数量关系，并说明理由；
（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
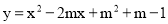（m是常数）的顶点为P，直线l：y=x﹣1（1）求证：点P在直线l上；
（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；
（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．
相关试题
