【题目】如图,已知矩形纸片ABCD中,AD=9cm,AB=3cm,将其折叠,使点D 与点B重合.
(1)求折叠后DE的长;
(2)求折痕EF的长.

参考答案:
【答案】(1)5;(2)![]()
【解析】试题分析:(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,根据勾股定理得出AE2+AB2=BE2,即(9-x)2+32=x2,解方程求出x,即可得出DE的长;
(2)连接BD,作EG⊥BC于G,则四边形ABGE是矩形,∠EGF=90°,得出EG=AB=3,BG=AE=4,得出GF=1,由勾股定理求出EF2,即可得出EF的长.
试题解析:(1)设DE长为xcm,则AE=(9-x)cm,BE=xcm,
∵四边形ABCD是矩形,
∴∠A=90°,
根据勾股定理得:AE2+AB2=BE2,
即(9-x)2+32=x2,
解得:x=5,
即DE长为5cm,
(2)作EG⊥BC于G,如图所示:
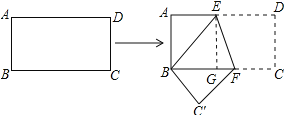
则四边形ABGE是矩形,∠EGF=90°,
∴EG=AB=3,BG=AE=4,
∴GF=1,
∴EF2=EG2+GF2=32+12=10,
∴EF=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
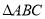 中,
中, 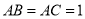 ,
,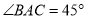 ,
, 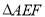 是由
是由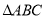 绕点
绕点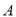 按顺时针方向旋转得到的,连接
按顺时针方向旋转得到的,连接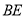 、
、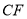 相交于点
相交于点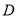 .
.(1)求证:
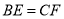 ;
;(2)当四边形
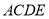 为菱形时,求
为菱形时,求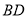 的长.
的长. 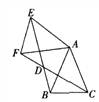
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
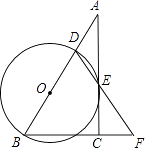
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,制作某金属工具先将材料煅烧6分钟温度升到800℃,再停止煅烧进行锻造,8分钟温度降为600℃;煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时温度y(℃)与时间x(min)成反比例函数关系;该材料初始温度是32℃.

(1)分别求出材料煅烧和锻造时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作,那么锻造的操作时间有多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x=
 .
.
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与C重合,折痕EF交AD于E,交BC于F,交AC于O,连结AF、CE.
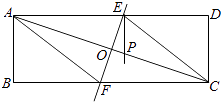
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:AE2=AOAP;
(3)若AE=8,△ABF的面积为9,求AB+BF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式:
 =
=  )( )
)( )
A.25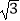 +75
+75
B.50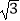 +50
+50
C.75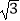 +75
+75
D.50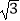 +100
+100
相关试题

