Question

【题目】如图，在矩形ABCD中，AB=3，BC=4，动点P以每秒一个单位的速度从点A出发，沿对角线AC向点C移动，同时动点Q以相同的速度从点C出发，沿边CB向点B移动．设P，Q两点移动时间为t秒（0≤t≤4）．

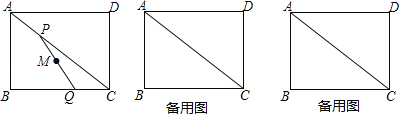
（1）用含t的代数式表示线段PC的长是 ；

（2）当△PCQ为等腰三角形时，求t的值；

（3）以BQ为直径的圆交PQ于点M，当M为PQ的中点时，求t的值．

Answer 1

【答案】（1）5﹣t；（2）当t=或t=或t=时，△PCQ为等腰三角形；（3）当M为PQ的中点时，t的值为．

【解析】

试题分析：（1）根据勾股定理求出AC，根据题意用t表示出AP，结合图形计算即可；

（2）分CP=CQ、QP=QC、PQ=PC三种情况，根据等腰三角形的性质和相似三角形的判定和性质计算即可；

（3）连接BP、BM，根据直径所对的圆周角是直角、等腰三角形的三线合一得到BP=BQ，根据勾股定理用t表示出BP、BQ，列出方程，解方程即可．

解：（1）∵∠B=90°，AB=3，BC=4，

∴AC=5，

∵点P的速度是每秒一个单位，移动时间为t秒，

∴AP=t，

则PC=AC﹣AP=5﹣t，

故答案为：5﹣t；

（2）当CP=CQ时，t=5﹣t，

解得t=，

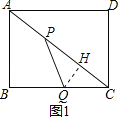
当QP=QC时，过点Q作QH⊥AC于H，如图1，

则PH=HC=PC=（5﹣t），QC=t，

∵QH⊥AC，∠B=90°，

∴△CHQ∽△CBA，

∴=，即=，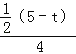

解得t=，

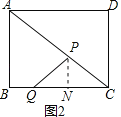
当PQ=PC时，如图2，

过点P作PN⊥QC于N，

则NC=NQ=QC=t，

∵△CPN∽△CAB，得

=，即=，

解得t=，

综上所述，当t=或t=或t=时，△PCQ为等腰三角形；

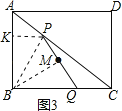
（3）连接BP、BM，如图3，则∠BMQ=90°，

∵M为PQ的中点，

∴BP=BQ，

过点P作PK⊥AB于K，

∵AP=t，

∴PK=t，AK=t，

∴BK=3﹣t，

在Rt△BPK中，PB2=PK2+BK2=（3﹣t）2+（t）2，又BQ=4﹣t，

∴（4﹣t）2=（3﹣t）2+（t）2，

解得t=．

∴以BQ为直径的圆交PQ于点M，当M为PQ的中点时，t的值为．