【题目】(本题满分12分)已知:点E为AB边上的一个动点.
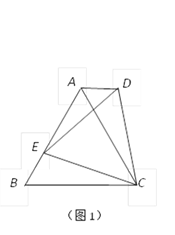
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC ,连结AD.试比较∠DAC与∠B的大小,并说明理由;
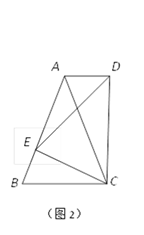
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC ,且
△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;
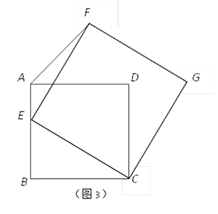
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.
参考答案:
【答案】(1)∠DAC=∠B 理由见解析;(2)AD∥BC 理由见解析;(3)点F的运动路径长为![]() .
.
【解析】解:(1) ∠DAC=∠B 理由如下:
∵△ABC和△DEC都是等边三角形 ∴∠DCE=∠ACB=60° ∴∠BCE=∠ACD
∵BC=AC CE=CD ∴△BCE≌△ACD ∴∠B=∠DAC
(2)AD∥BC 理由如下:
∵△ABC和△DEC都是等腰三角形,且△DEC∽△ABC ∴![]()
∵∠DCE=∠ACB ∴∠DCA=∠ECB ∴△DCA∽△ECB
∴∠DAC=∠EBC=∠ACB ∴AD∥BC
(3)①连结DG,∵四边形ABCD和FECG都是正方形
∴BC=CD CE=CG ∠BCD=∠ECG=90°
∴∠BCE=∠DCG∴△BCE≌△DCG …∴∠B=∠CDG=90°
∵∠ADC=90°∴∠ADC+∠CDG=180°
∴点G一定在AD的延长线上.
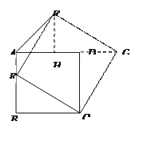
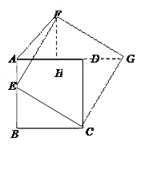
②作FH⊥AG于点H,易证:△FHG≌△GDC≌△EBC
∴FH=BE=DG HG=BC
∴AH=AG-GH=AD+DG-GH= BC+DG-BC=DG=FH
∴△AFH是等腰直角三角形
∴∠FAG=45°
∴点F的运动路径长=AC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在封闭图形ABCD附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),
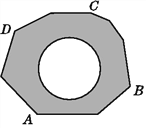
记录如下:
掷小石子所落的总次数
小石子所落的有效区域
50
150
300
…
小石子落在圆内(含圆上)的次数m
14
48
89
…
小石子落在圆以外的阴影部分(含外缘)的次数n
30
95
180
…
(1)当投掷的次数很大时,m∶n的值越来越接近___________(结果精确到0.1);
(2)若以小石子所落的有效区域里的次数为总数(即m+n),则随着投掷次数的增加,小石子落在圆内(含圆上)的频率稳定在___________附近;
(3)若你投一次石子,则小石子落在圆内(含圆上)的概率为___________;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,属于必然事件的是( )
A.明天我市下雨
B.抛一枚硬币,正面朝下
C.购买一张福利彩票中奖了
D.掷一枚骰子,向上一面的数字一定大于零 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:

(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C顺时针方向旋转60°,到△ADC,连接OD.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由.
(3)探索:当α为多少度时,△AOD是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
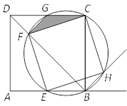
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
相关试题

