【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABCM的面积.

参考答案:
【答案】(1)、6;(2)、9.
【解析】
试题分析:(1)、由四边形ABCD为平行四边形,得到对边平行且相等,且对角线互相平分,根据两直线平行内错角相等得到两对角相等,进而确定出三角形MND与三角形CNB相似,由相似得比例,得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;(2)、由相似三角形相似比为1:2,得到S△MND:S△CND=1:4,可得到△MND面积为1,△MCD面积为3,由S平行四边形ABCD=ADh,S△MCD=MDh=ADh,=4S△MCD,即可求得答案.
试题解析:(1)、∵平行四边形ABCD, ∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC, ∴△MND∽△CNB, ∴![]() ,
,
∵M为AD中点,所以BN=2DN, 设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x﹣1,
∴x+1=2(x﹣1), 解得:x=3, ∴BD=2x=6;
(2)、∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=1:2, ∴S△MND:S△CND=1:4, ∵△DCN的面积为2, ∴△MND面积为1,
∴△MCD面积为3, 设平行四边形AD边上的高为h, ∵S平行四边形ABCD=ADh,S△MCD=MDh=ADh,
∴S平行四边形ABCD=4S△MCD=12. ∴四边形ABCM的面积=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2-4=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当 x=﹣1 时,代数式 2ax3﹣3bx+8 的值为 18,这时 6b﹣4a+2 的值为( )
A. 20 B. 22 C. ﹣18 D. ﹣22
-
科目: 来源: 题型:
查看答案和解析>>【题目】将(﹣3)3,(﹣3)4,(﹣3)5 从小到大排列正确的是( )
A. (﹣3)3<(﹣3)4<(﹣3)5 B. (﹣3)5<(﹣3)4<(﹣3)3 C. (﹣3)5<(﹣3)3<(﹣3)4 D. (﹣3)3<(﹣3)5<(﹣3)4
-
科目: 来源: 题型:
查看答案和解析>>【题目】双 11 来了,剁手的脚步近了,去年“双 11”期间,自 11 日到 16 日累计进出港快递量达到 16089000 件,同比增长 69.36%,数据 16089000 用科学记数法表示为_________.
-
科目: 来源: 题型:
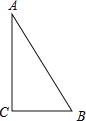
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,P为AB中点,BE⊥DP交DP延长线于E,连结AE,AF⊥AE交DP于F,连结BF,CF.下列结论:①EF=
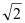 AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.
AF;②AB=FB;③CF∥BE;④EF=CF.其中正确的结论有( )个.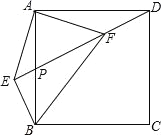
A.1 B.2 C.3 D.4
相关试题

