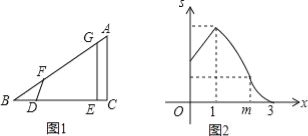
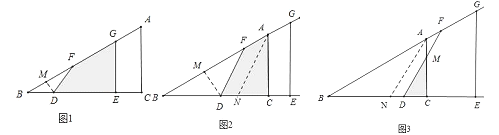
【题目】如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同)
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.
参考答案:
【答案】(1)3;(2)S=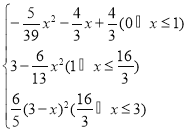 .
.
【解析】
试题分析:(1)由图象即可解决问题.(2)分三种情形:①如图1中,当0≤x≤1时,作DM⊥AB于M,根据S=S△ABC﹣S△BDF﹣S四边形ECAG即可解决.②如图2中,作AN∥DF交BC于N,设BN=AN=x,在RT△ANC中,利用勾股定理求出x,再根据S=S△ABC﹣S△BDF﹣S四边形ECAG即可解决.③如图3中,根据S=![]() CDCM,求出CM即可解决问题.
CDCM,求出CM即可解决问题.
试题解析:(1)由图象可知BC=3.
(2)①如图1中,当0≤x≤1时,作DM⊥AB于M,
由题意BC=3,AC=2,∠C=90°,
∴AB=![]() ,
,
∵∠B=∠B,∠DMB=∠C=90°,
∴△BMD∽△BCA,
∴![]() ,
,
∴DM=![]() ,BM=
,BM=![]() ,
,
∵BD=DF,DM⊥BF,
∴BM=MF,
∴S△BDF=![]() x2,
x2,
∵EG∥AC,
∴![]() ,
,
∴![]() ,
,
∴EG=![]() (x+2),
(x+2),
∴S四边形ECAG=![]() [2+
[2+![]() (x+2)](1﹣x),
(x+2)](1﹣x),
∴S=S△ABC﹣S△BDF﹣S四边形ECAG=3﹣![]() x2﹣
x2﹣![]() [2+
[2+![]() (x+2)](1﹣x)=﹣
(x+2)](1﹣x)=﹣![]() x2+
x2+![]() x+
x+![]() .
.
②如图②中,作AN∥DF交BC于N,设BN=AN=x,
在RT△ANC中,∵AN2=CN2+AC2,
∴x2=22+(3﹣x)2,
∴x=![]() ,
,
∴当1<x≤![]() 时,S=S△ABC﹣S△BDF=3﹣
时,S=S△ABC﹣S△BDF=3﹣![]() x2,
x2,
③如图3中,当![]() <x≤3时,
<x≤3时,
∵DM∥AN,
∴![]() ,
,
∴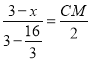 ,
,
∴CM=![]() (3﹣x),
(3﹣x),
∴S=![]() CDCM=
CDCM=![]() (3﹣x)2,
(3﹣x)2,
综上所述S=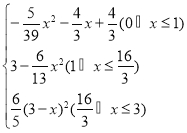 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对角线互相的平行四边形是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
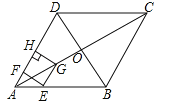
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中.有抛物线
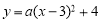 和
和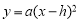 .抛物线
.抛物线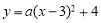 经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线
经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线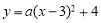 上一点,且在x轴上方.过点P作x轴的垂线交抛物线
上一点,且在x轴上方.过点P作x轴的垂线交抛物线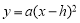 于点Q.过点Q作PQ的垂线交抛物线
于点Q.过点Q作PQ的垂线交抛物线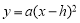 于点
于点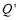 (不与点Q重合),连结
(不与点Q重合),连结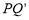 .设点P的横坐标为m.
.设点P的横坐标为m.
(1)求a的值;
(2)当抛物线
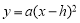 经过原点时,设△
经过原点时,设△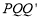 与△OAB重叠部分图形的周长为l.
与△OAB重叠部分图形的周长为l.①求
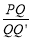 的值;
的值;②求l与m之间的函数关系式;
(3)当h为何值时,存在点P,使以点O、A、Q、
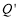 为顶点的四边形是轴对称图形?直接写出h的值.
为顶点的四边形是轴对称图形?直接写出h的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内定义运算“♀”,该运算同时满足下列条件:
(1)x♀x=5,(x≠5);(2)x♀(y♀z)=(x♀y)+z,则2015♀2017的值是( )
A. 2 B. 3 C. 2015 D. 2017
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断中,正确的序号为_______.
①若﹣a>b>0,则ab<0;②若ab>0,则a>0,b>0;③若a>b,c≠0,则ac>bc;④若a>b,c≠0,则ac2>bc2;⑤若a>b,c≠0,则﹣a﹣c<﹣b﹣c.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个连续的正奇数,最大数与最小数的积比中间一个数的6倍多3,求这三个数.
相关试题

