【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受人们的喜欢,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,2016年经过改造升级后A型车每辆销售价比2015年增加400元,若2016年6月份与2015年6月份卖出的A型车数量相同,则2016年6月份A型车销售总额将比2015年6月份销售总额增加25%.
(1)求2016年6月份A型车每辆销售价为多少元(用列方程的方法解答);
(2)该车行计划2016年7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格/(元/辆) | 1100 | 1400 |
销售价格/(元/辆) | 2016年的销售价格 | 2400 |
应如何进货才能使这批车获利最多?
参考答案:
【答案】(1)2016年6月份A型车每辆销售价为2000元.(2)进A型车17辆,B型车33辆,才能使这批车获利最多.
【解析】
(1)设2015年A型车每辆x元,那么2016年每辆(x+400)元,列出方程即可解决问题;(2)设2016年7月份进A型车m辆,则进B型车(50-m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题即可.
(1)3.2万元=32000元,设2015年6月份A型车每辆x元,那么2016年6月份每辆(x+400)元,根据题意得
![]() =
=![]() ,
,
解得x=1600,
经检验,x=1600是方程的解.
x+400=1600+400=2000(元).
答:2016年6月份A型车每辆销售价为2000元.
(2)设2016年7月份进A型车m辆,则进B型车(50-m)辆,获得的总利润为y元.
根据题意得50-m≤2m,
解得m≥16![]() .
.
y=(2000-1100)m+(2400-1400)(50-m)=-100m+50000,
∵-100<0,
∴y随m的增大而减小,
∴当m=17时,可以获得最大利润.
50-m=50-17=33.
答:进A型车17辆,B型车33辆,才能使这批车获利最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合).
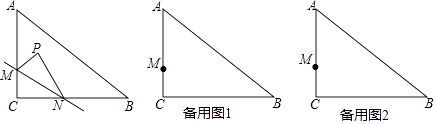
(1)若CM=2,
①又当点N在CB上,MP∥BC时,则CN= , MN=;
(2)在(1)的条件下,求点P到AB边的距离的最小值,并求出当取得这个最小值时,点P运动路线的长是多少?(参考数据:sin54°=cos36°≈ ,sin36°=cos54°≈
,sin36°=cos54°≈  ,结果保留π)
,结果保留π)
(3)设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲种原料130kg,乙种原料144kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5kg,乙种原料4kg,且每件A产品可获利700元;生产每件B产品需甲种原料3kg,乙种原料6kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种;
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(观察)方程
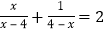 的解是
的解是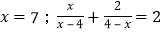 的解是
的解是 ;
;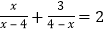 的解是
的解是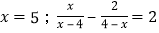 的解是
的解是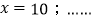
(发现)根据你的阅读回答问题:
(1)
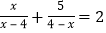 的解为_______;
的解为_______;(2)关于
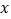 的方程
的方程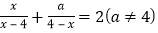 的解为_______(用含
的解为_______(用含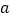 的代数式表示),并利用“方程的解的概念”验证.
的代数式表示),并利用“方程的解的概念”验证.(类比)
(3)关于
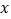 的方程
的方程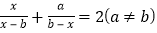 的解为_________(用含
的解为_________(用含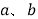 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算正确的是( )
A.3﹣1=﹣3
B.3﹣3=﹣9
C.3﹣2=
D.30=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
相关试题

