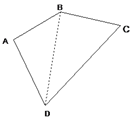
【题目】小明画了一个如图所示的四边形,其中AB=4,BC=12,CD=13,DA=3,∠A=![]() ,你能求出四边形ABCD的面积吗?
,你能求出四边形ABCD的面积吗?
参考答案:
【答案】36
【解析】试题分析: 先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
试题解析:
∵∠DAB=90°,
∴AB2+AD2=BD2.
∵AB=4,AD=3,
∴BD=5.
∵BC=12,CD=13,BD=5,
∴BD2+BC2=CD2.
∴△BCD为直角三角形.
∵∠DAB=90°,AB=4,AD=3,
∴S△ABD=![]() ×AB×AD=6.
×AB×AD=6.
∵△BCD为直角三角形,BC=12,BD=5,
∴S△BCD=12×BC×BD=30.
∵S四边形ABCD=S△ABD+S△BCD,S△ABD=6,S△BCD=30,
∴S四边形ABCD=36.
点睛: 本题考查了勾股定理、勾股定理的逆定理及三角形的面积;能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图(2),线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,张老师说:“
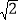 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把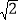 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(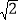 ﹣1)表示它的小数部分.接着,张老师出示了一道练习题:
﹣1)表示它的小数部分.接着,张老师出示了一道练习题:“已知8+
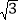 =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(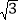 ﹣y)2016的值”.请聪明的你给出正确答案.
﹣y)2016的值”.请聪明的你给出正确答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x2=2x4
B.x4x2=x6
C.3x2÷x=2x
D.(x2)3=x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上的点A到原点的距离是6,则点A表示的数为( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形三个内角度数的比为1:2:3,则其内角度数最大的是( )
A. 60° B. 90° C. 120° D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班举办了一个集邮展览,展出的邮票若平均每人3张则多24张,若平均每人4张则少26张,则这个班学生有____人,一共展出的邮票有____张.
相关试题

