【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC交CD于E,DF平分∠ADC交AB于F.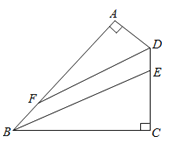
(1)若∠ABC=60°,则∠ADC= °,∠AFD=°;
(2)BE与DF平行吗?试说明理由.
参考答案:
【答案】
(1)120;30
(2)
解:BE∥DF.理由如下:
∵BE平分∠ABC交CD于E,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() ×60°=30°,
×60°=30°,
∵∠AFD=30°;
∴∠ABE=∠AFD,
∴BE∥DF.
【解析】(1)根据四边形内角和为360°可计算出∠ADC=120°,再根据角平分线定义得到∠FDA=![]() ADC=60°,然后利用互余可计算出∠AFD=30°;
ADC=60°,然后利用互余可计算出∠AFD=30°;
(2)先根据BE平分∠ABC交CD于E得∠ABE=![]() ∠ABC=30°,而∠AFD=30°则∠ABE=∠AFD,于是可根据平行线的判定方法得到BE∥DF.
∠ABC=30°,而∠AFD=30°则∠ABE=∠AFD,于是可根据平行线的判定方法得到BE∥DF.
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣5的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b,c,d,的极差为m,a+x,b+x,c+x,d+x的极差为_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一个月的月历中成一竖列的连续三个日期的和是33,这三天分别是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62 . 游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
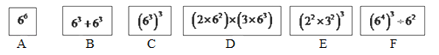
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )
A.外离
B.外切
C.相交
D.内切
相关试题

