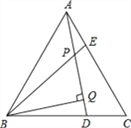
【题目】如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.PQ=4,PE=1
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数.
(3)求AD的长。
参考答案:
【答案】(1)见解析(2)60°;(3)9
【解析】【试题分析】
(1)根据等边三角形的性质,易得AB=AC,∠BAC=∠C=60°,因为AE=CD,根据SAS判定,易得△ABE≌△CAD;
(2)根据全等三角形的性质得,∠ABE=∠CAD,利用等量代换得:∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°;
(3) 在![]() 中,
中, ![]() 因为 PQ=4,所以BP=8,由于PE=1,所以BE=BP+PE=8+1=9,因为AD=BE,所以 AD=9.
因为 PQ=4,所以BP=8,由于PE=1,所以BE=BP+PE=8+1=9,因为AD=BE,所以 AD=9.
【试题解析】
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
AB=AC,∠BAC=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS);
(2)由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
(3)在![]() 中,
中, ![]()
![]() PQ=4,
PQ=4, ![]() ,
,
![]() BP=8,由于PE=1,
BP=8,由于PE=1,
![]() BE=BP+PE=8+1=9,
BE=BP+PE=8+1=9, ![]() AD=BE,
AD=BE, ![]() AD=9.
AD=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据2010年全国第六次人口普查数据公布,云南省宣威市常住人口为1420000人,1420000人用科学记数法表示为( )
A.1.42×104人
B.1.42×105人
C.1.42×106人
D.1.42×107人 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简|3.14﹣π|=( )
A.π﹣3.14
B.3.14+π
C.3.14﹣π
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
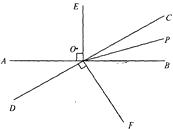
(1)图中除直角外,还有相等的角吗?请写出两对:①;② .
(2)如果∠AOD=40°,则①∠BOC=;②OP是∠BOC的平分线,所以∠COP=度;③求∠BOF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列所给线段长为三边,能构成直角三角形的是( )
A. 3cm、4cm、5cm B. 9cm、16cm、25cm
C. 5cm、12cm、15cm D. 8cm、15cm、16cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:
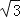 ≈1.732)
≈1.732)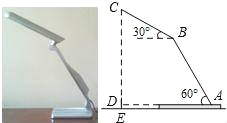
相关试题

