搜索
【题目】如图，函数y＝－x与函数y＝－
的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D，求四边形ACBD的面积．
参考答案：
【答案】8
【解析】根据函数y=-x与函数y=-
的图象相交于A，B两点，可以得到点A和点B的坐标，然后根据过A，B两点分别作y轴的垂线，垂足分别为点C，D，即可得到四边形ACBD的形状，然后根据平行四边形的面积公式即可解答本题．
∵函数y=-x与函数y=-的图象相交于A，B两点，
∴
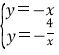,解得，
,或
，
∴点A的坐标为（-2，2），点B的坐标为（2，-2），
∵A，B两点分别作y轴的垂线，垂足分别为点C，D，
∴AC=BD=2，AC∥BD，CD=4，
∴四边形ADBC是平行四边形，
∴四边形ACBD的面积是2×4=8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数的序号填到相应的横线上:
①+5,②-3,③0,④-1.414,⑤17,⑥-
.正整数：______________________________________________________；
负分数：______________________________________________________；
负有理数：____________________________________________________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】某厂仓库储存了部分原料，按原计划每时消耗2 t，可用60 h．由于技术革新，实际生产能力有所提高，即每时消耗的原料量大于计划消耗的原料量．设现在每时消耗原料x(单位：t)，库存的原料可使用的时间为y(单位：h)．
(1)写出y关于x的函数解析式，并求出自变量的取值范围；
(2)若恰好经过24 h才有新的原料进厂，为了使机器不停止运转，则x应控制在什么范围内？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b的图象与反比例函数y=
的图象交于点A（﹣3，m+8），B（n，﹣6）两点．（1）求一次函数与反比例函数的解析式；
（2）求△AOB的面积．
-
科目： 来源： 题型：
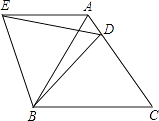
查看答案和解析>>【题目】在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列四个结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△AED的周长是9．其中正确的结论是（把你认为正确结论的序号都填上．）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝k1x＋7(k1＜0)与x轴交于点A，与y轴交于点B，与反比例函数y＝
(k2＞0)在第一象限的图象交于C，D两点，点O为坐标原点，△AOB的面积为
，点C的横坐标为1.(1)求反比例函数的解析式；
(2)如果一个点的横、纵坐标都是整数，那么我们就称这个点为“整点”，请求出图中阴影部分(不含边界)所包含的所有整点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某天早上，一辆交通巡逻车从A地出发，在东西向的马路上巡视，中午到达B地，如果规定向东行驶为正，向西行驶为负，行驶纪录如下:（单位：km）
第一次
第二次
第三次
第四次
第五次
第六次
第七次
+15
－8
+6
+12
－4
+5
－10
（1）B地在A地哪个方向，与A地相距多少千米？
（2）巡逻车在巡逻过程中，离开A地最远是多少千米？
（3）若每km耗油0.1升，问共耗油多少升？
相关试题
