【题目】如图，点A是双曲线y= 在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为（ ）
A.y=
B.y=
C.y=﹣
D.y=﹣

参考答案：

【答案】D
【解析】解：如图，连结OC，作CD⊥x轴于D，AE⊥x轴于E，
∵A点、B点是正比例函数图象与双曲线y= 的交点，
∴点A与点B关于原点对称，
∴OA=OB，
∵△ABC为等腰直角三角形，
∴OC=OA，OC⊥OA，
∴∠DOC+∠AOE=90°，
∵∠DOC+∠DCO=90°，
∴∠DCO=∠AOE，
∵在△COD和△OAE中，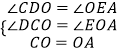
，
∴△COD≌△OAE（AAS），
设A点坐标为（a， ），则OD=AE= ，CD=OE=a，
∴C点坐标为（﹣ ，a），
∵﹣ a=﹣8，
∴点C在反比例函数y=﹣ 图象上．
故选（D）
先连结OC，作CD⊥x轴于D，AE⊥x轴于E，利用反比例函数的性质和等腰直角三角形的性质，根据“AAS”可判定△COD≌△OAE，设A点坐标为（a， ），得出OD=AE= ，CD=OE=a，最后根据反比例函数图象上点C的坐标特征确定函数解析式．

关闭