【题目】在平面直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴和y轴上,OA=3,OB=4.把△AOB绕点A顺时针旋转120°,得到△ADC.边OB上的一点M旋转后的对应点为M′,当AM′+DM取得最小值时,点M的坐标为( )

A. (0,![]() ) B. (0,
) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,3)
) D. (0,3)
参考答案:
【答案】A
【解析】
根据旋转的性质得到AM=AM′,得出AM′+DM的最小值=AM+DM的最小值,作点D关于直线OB的对称点D′,连接AD′交OB于M,则AD′=AM′+DM的最小值,过D作DE⊥x轴于E,解直角三角形得到DE=![]() ×3=
×3=![]() ,AE=
,AE=![]() ,求出D(
,求出D(![]() ,
,![]() ),根据轴对称的性质得到D′(
),根据轴对称的性质得到D′(![]() ,
,![]() ),求出直线AD′的解析式为y=
),求出直线AD′的解析式为y=![]() x+
x+![]() ,于是得到结论.
,于是得到结论.
∵把△AOB绕点A顺时针旋转120°,得到△ADC,点M是BO边上的一点,
∴AM=AM′,
∴AM′+DM的最小值=AM+DM的最小值,
作点D关于直线OB的对称点D′,连接AD′交OB于M,

则AD′=AM′+DM的最小值,
过D作DE⊥x轴于E,
∵∠OAD=120°,
∴∠DAE=60°,
∵AD=AO=3,
∴DE=![]() ×3=
×3=![]() ,AE=
,AE=![]() ,
,
∴D(![]() ,
,![]() ),
),
∴D′( ![]() ,
,![]() ),
),
设直线AD′的解析式为y=kx+b,
∴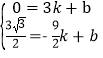 ,
,
∴
∴直线AD′的解析式为y=![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴M(0,![]() ),
),
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E是等边三角形ABC的边BC,AC上的点,且CD=AE,AD交BE于点P,BQ⊥AD于点Q,已知PE=2,PQ=6,则AD等于( )

A.10B.12C.14D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在一条直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.

(1)求证:AB=CD;
(2)若AB=CF,∠B=50°,求∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定,空气质量分为5级:当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1)本次调查共抽取了 天的空气质量检测结果,请补全条形统计图;
(2)扇形统计图中3级空气质量所对应的圆心角为 °;
(3)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,请你估计2015年该城市有多少天不适宜开展户外活动.(说明:2015年共365天)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
相关试题

