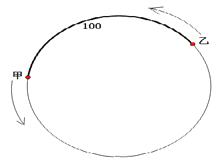
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为![]() 米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为
米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为![]() 秒.
秒.
(1)若![]() =5,求甲、乙两人第1次相遇的时间;
=5,求甲、乙两人第1次相遇的时间;
(2)当![]() 时,甲、乙两人第1次相遇.
时,甲、乙两人第1次相遇.
①求![]() 的值;
的值;
②若![]() 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求![]() 的值.
的值.
参考答案:
【答案】(1)t=100(2)① a=1或7 ②t=5或20
【解析】(1)根据相遇时,甲和乙的路程差等于200米列方程即可求解;
(2)①由第1次相遇时间为50秒,分两种情况:当![]() 时乙和甲的路程差等于100米;当
时乙和甲的路程差等于100米;当![]() 时甲和乙的路程差等于200米列方程即可求出a值;
时甲和乙的路程差等于200米列方程即可求出a值;
②当![]() 时由①可知a=7,分两种情况讨论:一种是乙距甲120米,即在100米的基础上甲又比乙多跑20米,此时两人在第一次相遇前相距120米,另一种是甲距乙120米,即在200米的基础上甲又比乙多跑80米,此时两人在第一次相遇前相距120米,即可得出t值.
时由①可知a=7,分两种情况讨论:一种是乙距甲120米,即在100米的基础上甲又比乙多跑20米,此时两人在第一次相遇前相距120米,另一种是甲距乙120米,即在200米的基础上甲又比乙多跑80米,此时两人在第一次相遇前相距120米,即可得出t值.
解:(1)由题可列方程![]() ,
,
解得: ![]() ,
,
答:若![]() =5,甲、乙两人第1次相遇的时间为100秒.
=5,甲、乙两人第1次相遇的时间为100秒.
(2)①有两种情况:
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
所以a=1或7;
②当![]() 时由①可知a=7,根据题意可列方程:
时由①可知a=7,根据题意可列方程:
![]() ,或
,或![]()
解得,t=5或20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某微生物的形状如球形,直径大约为0.00000109m,将0.000000109m用科学记数法表示为( )
A.1.09×10﹣6mB.1.09×10﹣7mC.10.9×10﹣7mD.1.09×10﹣8m
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
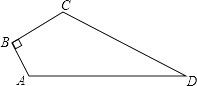
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两班共有88人,若从甲班调3人到乙班,那么两班人数正好相等,设甲班原有人数是x人,可列出方程( )
A.88﹣x=x﹣3
B.(88﹣x)+3=x﹣3
C.88+x=x﹣3
D.(88﹣x)+3=x -
科目: 来源: 题型:
查看答案和解析>>【题目】为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~100;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图1和如图2所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
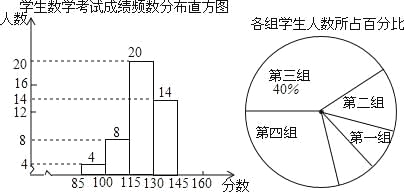
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1600名学生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组有两名女生和两名男生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意设未知数,并求出方程(不必求解):有两个工程队,甲队人数30名,乙队人数10名,问怎样调整两队的人数,才能使甲队的人数是乙队人数的7倍?
相关试题

