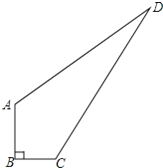
【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m,AD=12m,CD=13cm,求这块草地的面积.
参考答案:
【答案】36(m2).
【解析】
试题分析:连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出△CAD是直角三角形,分别求出△ABC和△CAD的面积,即可得出答案.
解:连结AC,
在△ABC中,
∵∠B=90°,AB=4m,BC=3m,
∴AC=![]() =5(m),
=5(m),
S△ABC=![]() ×3×4=6(m2),
×3×4=6(m2),
在△ACD中,
∵AD=12m,AC=5m,CD=13m,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD=![]() ×5×12=30(m2).
×5×12=30(m2).
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36(m2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的内角和是540°,那么这个多边形一定是正 边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个外角都等于36°,则该多边形的内角和等于_______度.
-
科目: 来源: 题型:
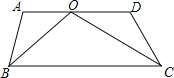
查看答案和解析>>【题目】如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=n°,则∠BOC= 度.
-
科目: 来源: 题型:
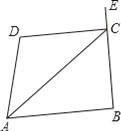
查看答案和解析>>【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°
(1)求∠DCA的度数;
(2)求∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小知识:如图,我们称两臂长度相等(即
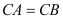 )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角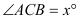 ,则底角
,则底角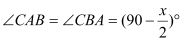 .
.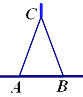
请运用上述知识解决问题:
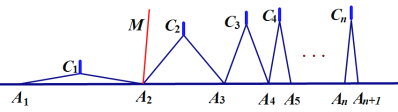
如图,
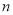 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下: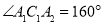 ,
,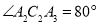 ,
, 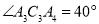 ,
,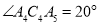 ,…
,…
(1)、①由题意可得
 = ;
= ;②若
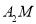 平分
平分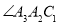 ,则
,则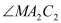 = ;
= ;(2)、
 = (用含
= (用含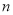 的代数式表示);
的代数式表示);(3)、当
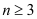 时,设
时,设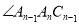 的度数为
的度数为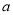 ,
,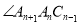 的角平分线
的角平分线 与
与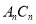 构成的角的度数为
构成的角的度数为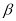 ,那么
,那么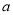 与
与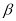 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)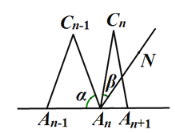
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋中装着3个红球和2个黄球,它们只有颜色上的区别,随机从袋中摸出1个小球,记下颜色不放回,再从袋子中任意取出1个小球,记下颜色:
(1)若取出的第一个小球为红色,则取出的第二个小球仍为红球的概率是 ;
(2)按要求从袋子中取出的两个球,请画出树状图或列表格,并求出取出的两个小球中有1个黄球、1个红球的概率.
相关试题

