【题目】已知![]() ,点
,点![]() 分别为两条平行线
分别为两条平行线![]() 上的一点,
上的一点,![]() 于
于![]() .
.
(1)如图1,直接写出![]() 和
和![]() 之间的数量关系;
之间的数量关系;
(2)如图2,连接![]() ,过点
,过点![]() 分别作
分别作![]() 和
和![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②探究![]() 和
和![]() 的数量关系并加以证明.
的数量关系并加以证明.

参考答案:
【答案】(1)![]() ,(2)①45°;②
,(2)①45°;②![]() ,证明见解析.
,证明见解析.
【解析】
(1)结论:∠ECD=90°+∠ABE.如图1中,过拐点作平行线,利用平行线性质即可得出结论;
(2) ①由![]() 和
和![]() 为
为![]() 和
和![]() 的角平分线,可得
的角平分线,可得![]() ,再由
,再由![]() ,通过角的运算即可得出结论.
,通过角的运算即可得出结论.
②由AB∥CD可得![]() ,再由
,再由![]() ,通过角的代换即可得出结论.
,通过角的代换即可得出结论.
解:(1)结论:![]() ,
,
理由:如图1中,从过G点作GH平行CD, 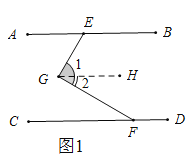
∵AB∥CD,
∴AB∥CD∥GH
∴∠AEG=∠1,∠CFG=∠2,
∵GE⊥GF,
∴∠CEH=90°,
∴∠ECD=∠H+∠CEH=90°+∠H,
∴∠ECD=90°+∠ABE.
(2)
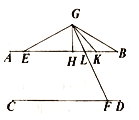
①∵![]()
∴![]() ,
,
∵![]() 和
和![]() 为
为![]() 和
和![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②结论:![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划用3300元购进甲,乙两种商品共100个,这两种商品的进价、售价如下表:
进价(元/个)
售价(元/个)
甲种
25
30
乙种
45
60
(1)求甲、乙两种商品各进多少个?
(2)全部售完100个商品后,该商场获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系
 中的点
中的点 ,给出如下定义:若存在点
,给出如下定义:若存在点 (
( 为正数),称点
为正数),称点 为点
为点 的等距点.例如:如图,对于点
的等距点.例如:如图,对于点 ,存在点
,存在点 ,点
,点 ,则点
,则点 分别为点
分别为点 的等距点.
的等距点.(1)若点
 的坐标是
的坐标是 ,写出当
,写出当 时,点
时,点 在第一象限的等距点坐标;
在第一象限的等距点坐标;(2)若点
 的等距点
的等距点 的坐标是
的坐标是 ,求当点
,求当点 的横、纵坐标相同时的坐标;
的横、纵坐标相同时的坐标;(3)是否存在适当的
 值,当将某个点
值,当将某个点 的所有等距点用线段依次连接起来所得到的图形周长不大于
的所有等距点用线段依次连接起来所得到的图形周长不大于 ,求
,求 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,四边形
中,四边形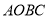 为边长为6的正方形,点
为边长为6的正方形,点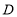 为
为 的中点,
的中点, .动点
.动点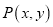 在线段
在线段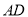 和
和 上运动,另一动点
上运动,另一动点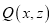 在线段
在线段 上运动.
上运动.用学过的知识解决下列问题:
(1)①填空:点
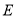 的坐标____________________;
的坐标____________________;②求三角形
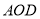 的面积;
的面积;(2)求点
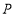 在运动过程中,
在运动过程中,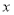 与
与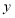 的数量关系;
的数量关系;(3)两个动点
 在运动过程中,是否存在使线段
在运动过程中,是否存在使线段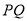 的长等于2的时刻,如果存在,求出此时点
的长等于2的时刻,如果存在,求出此时点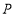 坐标;如果不存在,请你说明理由.
坐标;如果不存在,请你说明理由.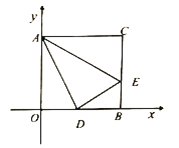
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
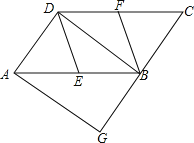
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于第一、三象限内的
的图像交于第一、三象限内的 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 在
在 轴负半轴上,
轴负半轴上, ,且四边形
,且四边形 是平行四边形,点
是平行四边形,点 的纵坐标为
的纵坐标为 .
.(1)求该反比例函数和一次函数的表达式;
(2)连接
 ,求
,求 的面积;
的面积;(3)直接写出关于
 的不等式
的不等式 的解集.
的解集.
相关试题

