【题目】如图1为某月的月历表,图2是![]() 型的框图,且框图中五个小正方形与月历表中每个小正方形大小相同.观察并思考下列问题:
型的框图,且框图中五个小正方形与月历表中每个小正方形大小相同.观察并思考下列问题:
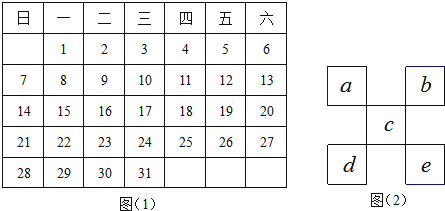
(1)用图2框图在月历表中任意圈出5个数(日期),这5个数的和的最小值是 ,最大值是 .
(2)在该月历表中可以得到 个这样的框图;
(3)如果型框图中5个数的和为80,则图二中字母a代表的数字是多少?并说明理由.
参考答案:
【答案】(1)45,115;(2)11;(3)a=8,理由见解析
【解析】
(1)根据题意可知:a最小时,5个数的和为最小,e最大时,5个数的和为最大;
(2)分类计算即可求出答案;
(3)根据图示中的等量关系列出方程即可求出答案.
解:(1)根据题意可知:a最小时,5个数的和为最小,
此时a=1,b=3,c=9,d=15,e=17,这5个数的和为45,
e最大时,5个数的和为最大,
此时a=15,b=17,c=23,d=29,e=31,这5个数的和为115;
(2)日历共有5行,其中第一行可以找出4个,
第二行可以找出5个,
第三行可以找出2个,故可以找出11个这样的图;
(3)由题意可知:a+(a+2)+(a+14)+(a+8)+(a+16)=80,
解得:a=8.
故答案为:(1)45,115;(2)11.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)观察下列图形与等式的关系,并填空:
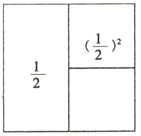
 +(
+( )2=1﹣(
)2=1﹣( )2;
)2;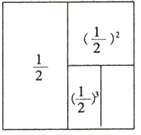
 +(
+( )2+(
)2+( )3=
)3= 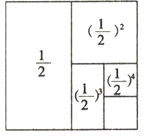
 +(
+( )2+(
)2+( )3+(
)3+( )4=
)4= (规律探究)观察下图:
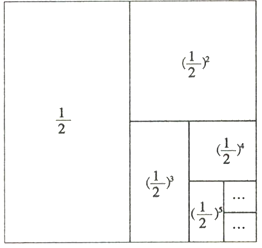
根据以上发现,用含n的代数式填空:
 +(
+( )2+(
)2+( )3+(
)3+( )4+(
)4+( )5+…+(
)5+…+( )n= .
)n= .(解决问题)根据以上发现,计算:
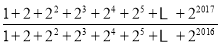 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
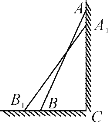
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,∠CAB=30°,∠CBA=45°,求AB的距离.(
 ≈1.41,
≈1.41,  ≈1.73,结果取整数)
≈1.73,结果取整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】王晓同学要证明命题“对角线相等的平行四边形是矩形”是正确的,她先作出了如图所示的平行四边形ABCD,并写出了如下不完整的已知和求证.

已知:如图,在平行四边形ABCD中, .
求证:平行四边形ABCD是 .
(1)在方框中填空,以补全已知和求证;
(2)按王晓的想法写出证明过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,左边是小颗的圆柱形笔筒,右边是小彬的六棱柱形笔筒,仔细观察两个笔简,并回答下面问题.

(1)圆柱、六棱柱各有几个面?
(2)圆柱的侧面与底面相交的线是直的还是曲的?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点(各写出一个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数,单位:万人),已知9月30日的游客人数为0.3万人,请回答下列问题:
日 期
1日
2日
3日
4日
5日
6日
7日
人数变化
+1.8
+0.8
+0.2
-0.4
-0.8
+0.2
-1.0
(1)七天内游客人数最多的是 日,最少的是 日;
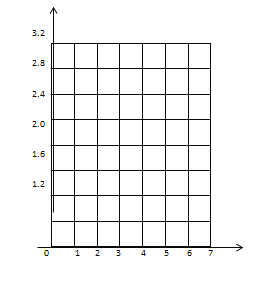
(2)若以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况?
(3)求这7天的游客人数是多少万人.
相关试题

