【题目】如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 面积记作S1;再作第二个正方形A2B2C2A3 , 面积记作S2;继续作第三个正方形A3B3C3A4 , 面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是 . 
参考答案:
【答案】1024
【解析】解:∵正方形A1B1C1A2 , ∠MON=45°, ∴△OA1B1是等腰直角三角形,
∴A1B1=OA1=1,
∴B1C1=A1B1=1,
又∵正方形形A1B1C1A2的边B1C1∥OA1 ,
∴∠MB1C1=45°,
同理可求B2C1=B1C1=1,
∴第二个正方形的边长为1+1=2,
同理可求出第三个正方形的边长为2+2=4=22 ,
…,
第6个正方形的边长为25 ,
∴第6个正方形的面积S6=(25)2=210=1024.
所以答案是:1024.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为A、B、C,且OA=OC=1,则下列关系中正确的是( )

A.a+b=﹣1
B.a﹣b=﹣1
C.b<2a
D.ac<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地相距450千米,两地之间有一个加油站O,且AO=270千米,一辆轿车从A地出发,以每小时90千米的速度开往B地,一辆客车从B地出发,以每小时60千米的速度开往A地,两车同时出发,设出发时间为t小时.
(1)经过几小时两车相遇?
(2)当出发2小时时,轿车和客车分别距离加油站O多远?
(3)经过几小时,两车相距50千米?
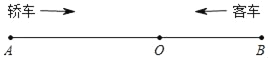
-
科目: 来源: 题型:
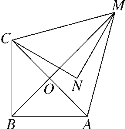
查看答案和解析>>【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=
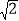 ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,点C,D分别是OA,AB的中点,△AOB的外角平分线与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=
 +1,则b=________.
+1,则b=________.(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
(4)直线AE与x轴交于点F,请用含b的式子直接写出点F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,木板的面积为( )

A. 60 B. 30 C. 24 D. 12
相关试题

