【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A
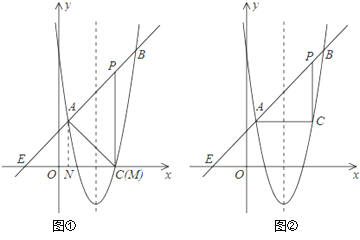
相交于A![]() 和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
(1)直接写出点B坐标;
(2)求抛物线的解析式;
(3)请用含m的代数式表示线段PC的长;
(4)若点P在线段AB上移动,请直接写出△PAC为直角三角形时点P的坐标.

参考答案:
【答案】(1)B(4,6),(2)抛物线的解析式为y=2x2﹣8x+6.(3)PC==2m2—9m+4;(4)点P的坐标为(3,5)或![]()
【解析】试题分析:(1)把点B(4,n)代入直线![]() 中即可求出n的值;(2)把点A、B的坐标代入抛物线
中即可求出n的值;(2)把点A、B的坐标代入抛物线![]() 中,得到一个关于a、b的二元一次方程组,解方程组即可,再写出抛物线的解析式;(3)设P点的横坐标为m,则点P的坐标为(m,m+2),点C的坐标为(m,2m2﹣8m+6);抛物线
中,得到一个关于a、b的二元一次方程组,解方程组即可,再写出抛物线的解析式;(3)设P点的横坐标为m,则点P的坐标为(m,m+2),点C的坐标为(m,2m2﹣8m+6);抛物线![]() 与x轴交点坐标为(4,0)和(
与x轴交点坐标为(4,0)和(![]() ,0),分两种情况求PC的长度:当点C在x轴上方时,即当
,0),分两种情况求PC的长度:当点C在x轴上方时,即当![]() <
<![]() 或
或![]() >4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;当点C在x轴下方时,即
>4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;当点C在x轴下方时,即![]() <
<![]() <4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;(3)图画即可写出;
<4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;(3)图画即可写出;
试题解析:
(1)B(4,6), (1分)
(2)∵A(![]() ,
,![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴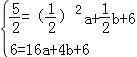 (3分)
(3分)
解得![]()
∴抛物线的解析式为y=2x2﹣8x+6. (4分)
(3)设动点P的坐标为(m,m+2),则C点的坐标为(m,2m2﹣8m+6),
当![]() <
<![]() <4时, (5分)
<4时, (5分)
PC=(m+2)﹣(2m2﹣8m+6),
=﹣2m2+9m﹣4 (6分)
当![]() <
<![]() 或
或![]() >4时, (7分)
>4时, (7分)
PC=(2m2﹣8m+6)—(m+2)
=2m2—9m+4 (8分)
(4)点P的坐标为(3,5)或![]() (10分)
(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班开展安全知识竞赛,评分标准是答对一道题得5分,记作+5分,答错或不答一道题扣2分,记作﹣2分.竞赛共有20道题,小明答对了15道题,则小明得分_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法求二次函数y=-x2+2x+1的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将自己的双手手掌印按在同一张纸上,两个手掌印____(填“能”或“不能”)通过平移完全重合在一起.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x-y=-5,z-y=11,则z-x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动,某中学为了了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图所示),请根据图中提供的信息,解答下列问题.

(1)m= %,这次共抽取 名学生进行调查;并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多?
(3)如果该校共有1500名学生,请你估计该校骑自行车上学的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x-3>1的解集是( )
A. x>2 B. x>4 C. x>-2 D. x>-4
相关试题

