【题目】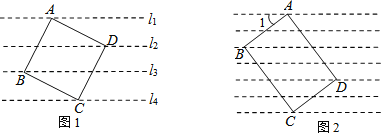
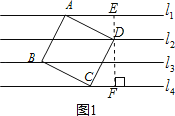
(1)如图1,4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线的距离都是2cm,正方形ABCD的4个顶点A、B、C、D分别在l1、l3、l4、l2上,求该正方形的面积;
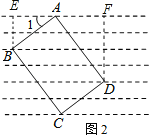
(2)如图2,把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中,恰好四个顶点都在横格线上,已知∠1=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
参考答案:
【答案】(1)正方形ABCD的面积为20cm2;(2)矩形ABCD的周长=300mm.
【解析】
试题分析:(1)过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,得CF=2,DF=4.根据勾股定理可求CD2得正方形的面积;
(2)作BE⊥l于点E,DF⊥l于点F,求∠ADF的度数,在Rt△ABE中,可以求得AB的值,在Rt△ADF中,可以求得AD的值,即可计算矩形ABCD的周长,即可解题.
解:(1)如图1,作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠AED=∠DFC=90°.
∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
在△ADE和△DCF,
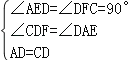 ,
,
∴△ADE≌△DCF(AAS),
∴CF=DE=2.
∵DF=4,
∴CD2=22+42=20,
即正方形ABCD的面积为20cm2;
(2)如图2,作BE⊥l于点E,DF⊥l于点F.
∵∠1+∠DAF=180°﹣∠BAD=180°﹣90°=90°,∠ADF+∠DAF=90°,
∴∠ADF=∠1=36°,
根据题意,得BE=36mm,DF=72mm.
在Rt△ABE中,sin∠1=![]() ,
,
∴AB=![]() =60mm,
=60mm,
在Rt△ADF中,cos∠ADF=![]() ,
,
∴AD=![]() mm=90mm.
mm=90mm.
∴矩形ABCD的周长=2(60+90)=300mm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1﹣2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=﹣2x的图象与反比例函数y=
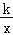 的图象交于点A(﹣1,n).
的图象交于点A(﹣1,n).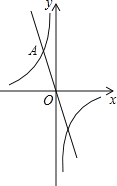
(1)求反比例函数y=
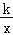 的解析式;
的解析式;(2)若P是x轴上一点,且△AOP是等腰三角形,求点P的坐标;
(3)结合图象直接写出不等式
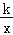 +2x>0的解集为 .
+2x>0的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=6,BC=7,点D,E分别在AB,AC上,DE∥BC.
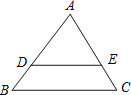
(1)当AD:DB=4:3时,求DE长;
(2)当△ADE的周长与四边形BCED的周长相等,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有1个点时,线段总共有3条,如果线段AB上有2个点时,线段总数有6条,如果线段AB上有3个点时,线段总数共有10条,…
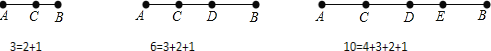
(1)当线段AB上有6个点时,线段总数共有 条.
(2)当线段AB上有n个点时,线段总数共有 条。
(3)如果从一个多边形的一个顶点出发,分别连接这个顶点与其余各顶点,可将这个多边形分割成2003个三角形,那么此多边形的边数为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用橡皮泥做一个棱长为4cm的正方体.

(1)如图(1),在顶面中心位置处从上到下打一个边长为1cm的正方体通孔,打孔后的橡皮泥的表面积为 cm2;
(2)如果在第(1)题打孔后,再在正面中心位置处(按图(2)中的虚线)从前到后打一个边长为1cm的正方体通孔,那么打孔后的橡皮泥的表面积为 cm2;
(3)如果把第(2)题中从前到后所打的正方形通孔扩大成一个长xcm、宽1cm的长方形通孔,能不能使所得橡皮泥的表面积为130cm2?如果能,请求出x;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国2016年第一季度GDP总值经初步核算大约为159000亿元,数据159000用科学记数法表示为 .
相关试题

