【题目】(1)已知关于x的方程kx=11﹣2x有整数解,则负整数k的值为 .
(2)若a+b+c=0,且a>b>c,以下结论:
①a>0,c>0;
②关于x的方程ax+b+c=0的解为x=1;
③a2=(b+c)2;
④![]() 的值为0或2;
的值为0或2;
⑤在数轴上点A、B、C表示数a、b、c,若b<0,则线段AB与线段BC的大小关系是AB>BC.
其中正确的结论是 (填写正确结论的序号).
参考答案:
【答案】(1)﹣1,﹣3,﹣13;(2)②③⑤.
【解析】
(1)解方程kx=11-2x,得出x=![]() ,根据方程有整数解,得出k+2是11的约数,求出k的值,再根据k为负整数即可确定k;
,根据方程有整数解,得出k+2是11的约数,求出k的值,再根据k为负整数即可确定k;
(2)根据a+b+c=0,且a>b>c推出a>0,c<0,即可判断①;
根据a+b+c=0求出a=-(b+c),又ax+b+c=0时ax=-(b+c),方程两边都除以a即可判断②;
根据a=-(b+c)两边平方即可判断③;
分为两种情况:当b>0,a>0,c<0时,去掉绝对值符号得出![]() ,求出结果,当b<0,a>0,c<0时,去掉绝对值符号得出
,求出结果,当b<0,a>0,c<0时,去掉绝对值符号得出![]() ,求出结果,即可判断④;
,求出结果,即可判断④;
求出AB=a-b=-b-c-b=-2b-c=-3b+b-c,BC=b-c,根据b<0利用不等式的性质即可判断⑤.
(1)解方程kx=11﹣2x,得x=![]() ,
,
∵方程有整数解,
∴k+2=1,﹣1,11,﹣11,
∴k=﹣1,﹣3,9,﹣13,
∵k为负整数,
∴k=﹣1,﹣3,﹣13.
故答案为﹣1,﹣3,﹣13;
(2)∵a+b+c=0,且a>b>c,
∴a>0,c<0,∴①错误;
∵a+b+c=0,a>b>c,
∴a>0,a=﹣(b+c),
∵ax+b+c=0,
∴ax=﹣(b+c),
∴x=1,∴②正确;
∵a=﹣(b+c),
∴两边平方得:a2=(b+c)2,∴③正确;
∵a>0,c<0,
∴分为两种情况:
当b>0时,![]() =
=![]() =1+1+(﹣1)+(﹣1)=0;
=1+1+(﹣1)+(﹣1)=0;
当b<0时,![]() =
=![]() =1+(﹣1)+(﹣1)+1=0;
=1+(﹣1)+(﹣1)+1=0;
∴④错误;
∵a+b+c=0,且a>b>c,b<0,
∴a>0,c<0,a=﹣b﹣c,
∴AB=a﹣b=﹣b﹣c﹣b=﹣2b﹣c=﹣3b+b﹣c,BC=b﹣c,
∵b<0,
∴﹣3b>0,
∴﹣3b+b﹣c>b﹣c,
∴AB>BC,∴⑤正确;
即正确的结论有②③⑤,
故答案为:②③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x+2(5﹣3x)=15﹣3(7﹣5x)
(2)

(3)
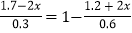
(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
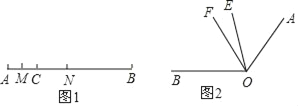
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
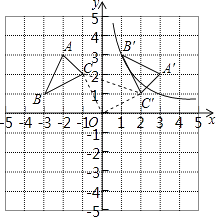
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为
 、
、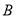 、
、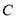 、
、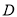 .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.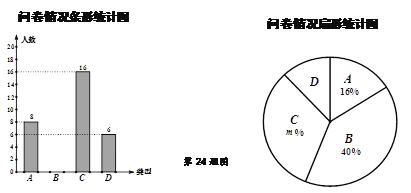
(1)本次问卷共随机调查了 名市民,扇形统计图中
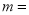 .
.(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE=4,连接EF交CD于G.若
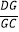 =
=  ,求AD的长.
,求AD的长. 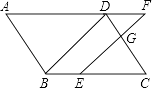
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直径坐标系中,反比例函数y=
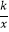 (x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=
(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD= 
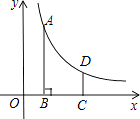
(1)点D的横坐标为(用含m的式子表示);
(2)求反比例函数的解析式.
相关试题

