Question

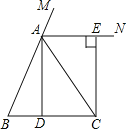
【题目】已知：如图，在△ABC中，AB=AC，点D为BC中点，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．求证：四边形ADCE为矩形．

Answer 1

【答案】证明见解析.

【解析】试题分析：根据AN是△ABC外角∠CAM的平分线，推得∠MAE=（∠B+∠ACB），再由∠B=∠ACB，得∠MAE=∠B，则AN∥BC，根据CE⊥AN，得出四边形ADCE为矩形．

证明：∵AN是△ABC外角∠CAM的平分线，

∴∠MAE=∠MAC，

∵∠MAC=∠B+∠ACB，

∵AB=AC，

∴∠B=∠ACB，

∴∠MAE=∠B，

∴AN∥BC，

∵AB=AC，点D为BC中点，

∴AD⊥BC，

∵CE⊥AN，

∴AD∥CE，

∴四边形ADCE为平行四边形（有两组对边分别平行的四边形是平行四边形），

∵CE⊥AN，

∴∠AEC=90°，

∴四边形ADCE为矩形（有一个角是直角的平行四边形是矩形）．