【题目】如图,已知在等腰Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE, 
(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当 ![]() =
= ![]() 时,求x的值.
时,求x的值.
参考答案:
【答案】
(1)证明:如图1,

由折叠可得:∠EDF=∠C=90°,∠DFE=∠CFE.
∵△ABC是等腰直角三角形,∠C=90°,
∴∠A=∠B=45°.
∵DK⊥AB,
∴∠ADK=∠BDK=90°,
∴∠AKD=45°,∠EDF=∠KDB=90°,
∴∠EKD=∠FBD,∠EDK=∠FDB,
∴△DEK∽△DFB;
(2)解:∵∠A=∠AKD=45°,
∴DK=DA=x.
∵AB=2,
∴DB=2﹣x.
∵△DFB∽△DEK,
∴ ![]() =
= ![]() ,
,
∴y=cot∠CFE=cot∠DFE= ![]() =
= ![]() =
= ![]() .
.
当点F在点B处时,
DB=BC=ABsinA=2× ![]() =
= ![]() ,AD=AB﹣AD=2﹣
,AD=AB﹣AD=2﹣ ![]() ;
;
当点E在点A处时,
AD=AC=ABcosA=2× ![]() =
= ![]() ;
;
∴该函数的解析式为y= ![]() ,定义域为2﹣
,定义域为2﹣ ![]() <x<
<x< ![]()
(3)取线段EF的中点O,连接OC、OD,
∵∠ECF=∠EDF=90°,
∴OC=OD= ![]() EF.
EF.
设EF与CD交点为H,根据轴对称的性质可得EF⊥CD,且CH=DH= ![]() CD.
CD.
∵ ![]() =
= ![]() ,∴sin∠HOC=
,∴sin∠HOC= ![]() =
= ![]() ,
,
∴∠HOC=60°
① 若点K在线段AC上,如图2,

∵CO= ![]() EF=OF,
EF=OF,
∴∠OCF=∠OFC= ![]() ∠HOC=30°,
∠HOC=30°,
∴y=cot30°= ![]() ,
,
∴ ![]() =
= ,
解得:x= ![]() ﹣1;
﹣1;
②若点K在线段AC的延长线上,如图3,

∵OC=OF,∠FOC=60°,
∴△OFC是等边三角形,
∴∠OFC=60°,
∴y=cot60°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:x=3﹣ ![]() ;
;
综上所述:x的值为 ![]() ﹣1或3﹣
﹣1或3﹣ ![]()
【解析】(1)要证△DEK∽△DFB,只需证到∠EKD=∠FBD,∠EDK=∠FDB即可;(2)易得DK=DA=x,DB=2﹣x,由△DFB∽△DEK可得到 ![]() =
= ![]() ,从而可得y=cot∠CFE=cot∠DFE=
,从而可得y=cot∠CFE=cot∠DFE= ![]() =
= ![]() =
= ![]() ;然后只需先求出在两个临界位置(点F在点B处、点E在点A处)下的x值,就可得到该函数的定义域;(3)取线段EF的中点O,连接OC、OD,根据直角三角形斜边上的中线等于斜边的一半可得OC=OD=
;然后只需先求出在两个临界位置(点F在点B处、点E在点A处)下的x值,就可得到该函数的定义域;(3)取线段EF的中点O,连接OC、OD,根据直角三角形斜边上的中线等于斜边的一半可得OC=OD= ![]() EF.设EF与CD交点为H,根据轴对称的性质可得EF⊥CD,且CH=DH=
EF.设EF与CD交点为H,根据轴对称的性质可得EF⊥CD,且CH=DH= ![]() CD.由
CD.由 ![]() =
= ![]() 可得tan∠HOC=
可得tan∠HOC= ![]() =
= ![]() ,从而得到∠HOC=60°.①若点K在线段AC上,如图2,由∠HOC=60°可求得∠OFC=30°,由此可得到y的值,再把y的值代入函数解析式就可求出x的值;②若点K在线段AC的延长线上,如图3,由∠HOC=60°可求得∠OFC=60°,由此可得到y的值,再把y的值代入函数解析式就可求出x的值.
,从而得到∠HOC=60°.①若点K在线段AC上,如图2,由∠HOC=60°可求得∠OFC=30°,由此可得到y的值,再把y的值代入函数解析式就可求出x的值;②若点K在线段AC的延长线上,如图3,由∠HOC=60°可求得∠OFC=60°,由此可得到y的值,再把y的值代入函数解析式就可求出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC.
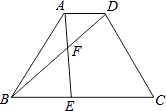
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,

(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
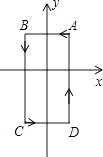
A.(﹣1,0)
B.(1,﹣2)
C.(1,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣1﹣20140﹣2sin30°+
)﹣1﹣20140﹣2sin30°+  .
.
相关试题

