【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售是600件,而销售单价每涨1元,就会少售出10件玩具.设该种品牌玩具的销售单价为x元(x>40),销售量为y件,销售该品牌玩具获得的利润为w元.
(1)根据题意,填写下表:
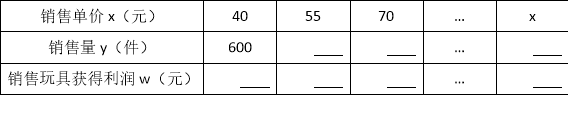
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元?
(3)在(1)问条件下,求商场销售该品牌玩具获得的最大利润是多少?此时玩具的销售单价应定为多少?
参考答案:
【答案】(1)答案见解析;(2)50元或80元;(3)商场销售该品牌玩具获得的最大利润是12250元,此时玩具的销售单价应定为65元.
【解析】
试题分析:(1)利用销售单价每涨1元,就会少售出10件玩具,再结合每件玩具的利润乘以销量=总利润进而求出即可;
(2)利用商场获得了10000元销售利润,进而得出等式求出即可;
(3)利用每件玩具的利润乘以销量=总利润得出函数关系式,进而求出最值即可.
试题解析:(1)填表:
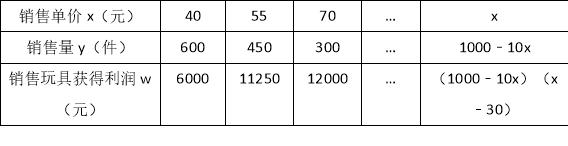
(2)[600﹣10(x﹣40)](x﹣30)=10000,解得:x1=50,x2=80,答:该玩具销售单价x应定为50元或80元;
(3)w=[600﹣10(x﹣40)](x﹣30)=﹣10x2+1300x﹣30000=﹣10(x﹣65)2+12250,∵a=﹣10<0,∴对称轴为x=65,∴当x=65时,W最大值=12250(元)
答:商场销售该品牌玩具获得的最大利润是12250元,此时玩具的销售单价应定为65元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2,宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF,现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为α.
(1)当边CD′恰好经过EF的中点H时,求旋转角α的大小;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△BCD′能否全等?若能,直接写出旋转角α的大小;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )

A.a=2b
B.a=3b
C.a=4b
D.a=b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知3a=5,9b=10,则3a+2b等于( )
A. -50 B. 50 C. 500 D. 无法确定
-
科目: 来源: 题型:
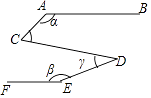
查看答案和解析>>【题目】如图,AB∥EF,∠C=60°,∠A=α,∠E=β,∠D=γ,则α、β、γ的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m﹣2n=﹣1,则代数式1﹣2m+4n的值是( )
A.﹣3
B.﹣1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】据测算,我国每天土地沙漠化造成的经济损失平均为150 000 000元,这个数字用科学记数法表示为( )
A.15×107元B.1.5×108元C.0.15×109元D.1.5×107元
相关试题

