Question

【题目】在平面直角坐标系xOy中，抛物线经过点A（0，2）和B（1，）．

（1）求该抛物线的表达式；

（2）已知点C与点A关于此抛物线的对称轴对称，点D在抛物线上，且点D的横坐标为4，求点C与点D的坐标；

（3）在（2）的条件下，将抛物线在点A，D之间的部分（含点A，D）记为图象G，如果图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点，求t的取值范围．

Answer 1

【答案】（1）y=x2﹣x+2；（2）C点坐标为（2，2）；D点坐标为（4，6）；（3）当1＜t≤3时，图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点．

【解析】

试题分析：（1）把A点和B点坐标代入得到关于b、c的方程组，然后解方程组求出b、c即可得到抛物线解析式；

（2）利用配方法得到y=（x﹣1）2+，则抛物线的对称轴为直线x=1，利用点C与点A关于直线x=1对称得到C点坐标为（2，2）；然后利用二次函数图象上点的坐标特征求D点坐标；

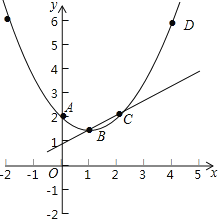
（3）画出抛物线，如图，先利用待定系数法求出直线BC的解析式为y=x+1，再利用平移的性质得到图象G向下平移1个单位时，点A在直线BC上；图象G向下平移3个单位时，点D在直线BC上，由于图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点，所以1＜t≤3．

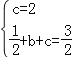解：（1）把A（0，2）和B（1，）代入得，解得，

所以抛物线解析式为y=x2﹣x+2；

（2）∵y=x2﹣x+2=（x﹣1）2+，

∴抛物线的对称轴为直线x=1，

∵点C与点A关于此抛物线的对称轴对称，

∴C点坐标为（2，2）；

当x=4时，y=x2﹣x+2=8﹣4+2=6，

∴D点坐标为（4，6）；

（3）如图，

设直线BC的解析式为y=mx+n，

把B（1，），C（2，2）代入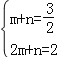得，解得，

∴直线BC的解析式为y=x+1，

当x=0时，y=x+1=1，

∴点图象G向下平移1个单位时，点A在直线BC上，

当x=4时，y=x+1=3，

∴点图象G向下平移3个单位时，点D在直线BC上，

∴当1＜t≤3时，图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点．