【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a﹣4|+ ![]() =0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)点B的坐标为 , 当点P移动3.5秒时,点P的坐标;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)在移动过程中,当△OBP的面积是10时,求点P移动的时间.
参考答案:
【答案】
(1)(4,6),(1,6)
(2)解:由题意可得,在移动过程中,当点P到x轴的距离为4个单位长度时,存在两种情况,
第一种情况,当点P在OC上时,
点P移动的时间是:4÷2=2秒,
第二种情况,当点P在BA上时.
点P移动的时间是:(6+4+2)÷2=6秒,
故在移动过程中,当点P到x轴的距离为4个单位长度时,点P移动的时间是2秒或6秒.
(3)解:如图1所示:

∵△OBP的面积=10,
∴ ![]() OPBC=10,即
OPBC=10,即 ![]() ×4×OP=10.
×4×OP=10.
解得:OP=5.
∴此时t=2.5s
如图2所示;

∵△OBP的面积=10,
∴ ![]() PBOC=10,即
PBOC=10,即 ![]() ×6×PB=10.
×6×PB=10.
解得:BP= ![]() .
.
∴CP= ![]() .
.
∴此时t= ![]() s,
s,
如图3所示:

∵△OBP的面积=10,
∴ ![]() BPBC=10,即
BPBC=10,即 ![]() ×4×PB=10.
×4×PB=10.
解得:BP=5.
∴此时t= ![]() s
s
如图4所示:

∵△OBP的面积=10,
∴ ![]() OPAB=10,即
OPAB=10,即 ![]() ×6×OP=10.
×6×OP=10.
解得:OP= ![]() .
.
∴此时t= ![]() s
s
综上所述,满足条件的时间t的值为2.5s或 ![]() s或
s或 ![]() s或
s或 ![]() s.
s.
【解析】(1)∵a、b满足 ![]() +|b﹣6|=0,
+|b﹣6|=0,
∴a﹣4=0,b﹣6=0,
解得a=4,b=6,
∴点B的坐标是(4,6),
∵点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动,
∴2×3.5=7,
∵OA=4,OC=6,
∴当点P移动4秒时,在线段CB上,离点C的距离是:7﹣6=1,
即当点P移动4秒时,此时点P在线段CB上,离点C的距离是2个单位长度,点P的坐标是(1,6);
所以答案是(4,6)|(1,6);
(2)P到x轴的距离为4个单位长度时,需分类讨论:点P在OC上和点P在BA上两种情况;
(3)△OBP的面积是10时,需分四种情况讨论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校将周五上午大课间活动项目定为跳绳活动,为此学校准备购置长、短两种跳绳若干.已知长跳绳的单价比短跳绳单价的三倍少4元,且购买2条长跳绳与购买5条短跳绳的费用相同.
(1)两种跳绳的单价各是多少元?
(2)若学校准备用不超过1950元的现金购买190条长、短跳绳,且短跳绳的条数不超过长跳绳的5倍,问学校有几种购买方案可供选择?并写出这几种方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论: ①EF=BE+CF;
②∠BGC=90°+ ∠A;
∠A;
③点G到△ABC各边的距离相等;
④设GD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边BC 为边做等边△BCE,则∠AED的度数为 _____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线
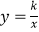 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 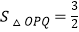 ,则k的值是( )
,则k的值是( )
A.4
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣2)2+1的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连接AD,若∠B=35°,求∠CAD的度数.
相关试题

