【题目】如图,已知数轴上点A,B是数轴上的一点,AB=12,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,经t秒后点P走过的路程为(用含t的代数式表示);
(2)若在动点P运动的同时另一动点Q从点B也出发,并以每秒4个单位长度的速度沿数轴向左匀速运动,问经多少时间点P就能追上点Q?
(3)若M为AP的中点,N为BP的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
参考答案:
【答案】解:(1)设B点表示x,则有
AB=8﹣x=12,解得x=﹣4.
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴经t秒后点P走过的路程为6t.
故答案为:﹣4;6t.
(2)设经t秒后P点追上Q点,根据题意得:
6t﹣4t=12,
解得t=6.
答:经过6秒时间点P就能追上点Q.
(3)不论P点运动到哪里,线段MN都等于6.
分两种情况分析:
①点P在线段AB上时,如图1,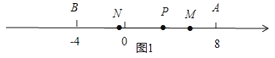
MN=PM+PN=![]() PA+
PA+![]() PB=
PB=![]() (PA+PB)=
(PA+PB)=![]() AB=
AB=![]() ×12=6;
×12=6;
②点P在线段AB的延长线上时,如图2,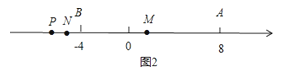
MN=PM﹣PN=![]() PA﹣
PA﹣![]() PB=
PB=![]() (PA﹣PB)=
(PA﹣PB)=![]() AB=
AB=![]() ×12=6.
×12=6.
综上可知,不论P运动到哪里,线段MN的长度都不变,都等于6.
【解析】(1)设出B点表示的数为x,由数轴上两点间的距离即可得到x的方程,解方程即可得出x,由路程=速度×时间可得出点P走过的路程;
(2)设经t秒后P点追上Q点,根据题意可得,关于t的一元一次方程,解方程即可得出时间t;
(3)由P点位置的不同分两种情况考虑,依据中点的定义,可以找到线段间的关系,从而能找出MN的长度.
【考点精析】认真审题,首先需要了解数轴(数轴是规定了原点、正方向、单位长度的一条直线).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣3y=3,则5﹣x+3y的值是( )
A.8
B.2
C.﹣2
D.﹣8 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列写法正确的是( )
A. 过点A、B画直线ab B. 直线AB、CD相交于点m
C. 直线ab、cd相交于点M D. 直线a、b相交于点M
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的2016年1月份的月历表中,用一个3×2的长方形框围住相邻三列两行中的6个数字,设其中第一行中间的数字为x.
(1)用含x的式子表示长方形框中6个数字的和
(2)若长方形框中6个数字的和是153,那么这6个数字分别是哪些数字?
(3)长方形框中6个数字的和能是117吗?简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:
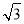 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果线段AB=10cm,AC+BC=20cm,则下列说法正确的是( )
A. 点C在线段AB上 B. 点C不能在直线AB上
C. 点C只能在直线AB上 D. 点C可能在直线AB上,也可能在直线AB外
相关试题

