【题目】如图,在平面直角坐标系中,函数![]() 的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
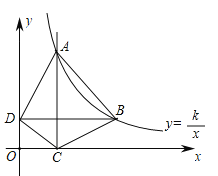
(1)求k的值
(2)若△ABD的面积为4;
①求点B的坐标,
②在平面内存在点E,使得以点A、B、C、E为顶点的四边形是平行四边形,直接写出符合条件的所有点E的坐标.
参考答案:
【答案】(1)4;(2)①(3,![]() ),②(3,
),②(3,![]() );(3,
);(3,![]() );(3,-
);(3,-![]() )
)
【解析】
(1)由点A的坐标,利用反比例函数图象上点的坐标特征可求出k值;
(2)①设AC,BD交于点M,利用反比例函数图象上点的坐标特征可得出点B的坐标,结合AC⊥x轴,BD⊥y轴可得出BD,AM的长,利用三角形的面积公式结合△ABD的面积为4可求出a的值,进而可得出点B的坐标;
②设点E的坐标为(m,n),分AB为对角线、AC为对角线以及BC为对角线三种情况考虑,利用平行四边形的性质(对角线互相平分)可得出关于m,n的二元一次方程组,解之即可得出点E的坐标.
解:(1)∵函数y=![]() (x>0)的图象经过点A(1,4),
(x>0)的图象经过点A(1,4),
∴k=1×4=4.
(2)①设AC,BD交于点M,如图1所示.
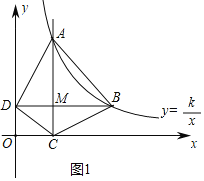
∵点B的横坐标为a(a>1),点B在y=![]() 的图象上,
的图象上,
∴点B的坐标为(a,![]() ).
).
∵AC⊥x轴,BD⊥y轴,
∴BD=a,AM=AC-CM=4-![]() .
.
∵△ABD的面积为4,
∴![]() BDAM=4,即a(4-
BDAM=4,即a(4-![]() )=8,
)=8,
∴a=3,
∴点B的坐标为(3,![]() )
)
②存在,设点E的坐标为(m,n).
分三种情况考虑,如图2所示.
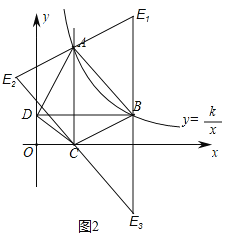
(i)当AB为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴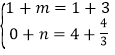 ,解得:
,解得: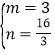 ,
,
∴点E1的坐标为(3,![]() );
);
(ii)当AC为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴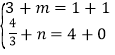 ,解得:
,解得: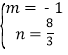 ,
,
∴点E2的坐标为(3,![]() );
);
(iii)当BC为对角线时,∵A(1,4),B(3,![]() ),C(1,0),
),C(1,0),
∴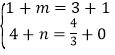 ,解得:
,解得: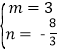 ,
,
∴点E2的坐标为(3,-![]() ).
).
综上所述:点E的坐标为(3,![]() );(3,
);(3,![]() );(3,-
);(3,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE∥BC

(1)求证:DE=CE;
(2)若∠A=90°,S△BCD=26,BC=13,求AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在正方形ABCD中,点E在对角线AC上(不与点A、C重合),连结ED,EB,过点E作EF⊥ED,交边BC于点F.易知∠EFC+∠EDC=180°,进而证出EB=EF.
探究:如图②,点E在射线CA上(不与点A、C重合),连结ED、EB,过点E作EF⊥ED,交CB的延长线于点F.求证:EB=EF
应用:如图②,若DE=2,CD=1,则四边形EFCD的面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于
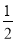 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )
A. 65°B. 60°C. 55°D. 45°
-
科目: 来源: 题型:
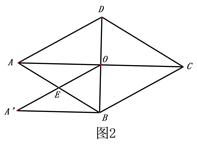
查看答案和解析>>【题目】如图1,菱形ABCD,AB=4,∠ADC=120o,连接对角线AC、BD交于点O,
(1)如图2,将△AOD沿DB平移,使点D与点O重合,求平移后的△A′BO与菱形ABCD重合部分的面积.
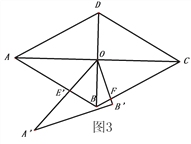
(2)如图3,将△A′BO绕点O逆时针旋转交AB于点E′,交BC于点F,
①求证:BE′+BF=2,
②求出四边形OE′BF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,l1反映了某公司销售一种医疗器械的销售收入(万元)与销售量(台)之间的关系,l2反映了该公司销售该种医疗器械的销售成本(万元)与销售量(台)之间的关系.当销售收入大于销售成本时,该医疗器械才开始赢利.根据图象,则下列判断中错误的是( )
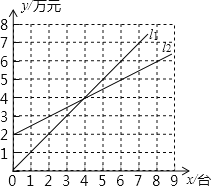
A. 当销售量为4台时,该公司赢利4万元
B. 当销售量多于4台时,该公司才开始赢利
C. 当销售量为2台时,该公司亏本1万元
D. 当销售量为6台时,该公司赢利1万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=
 ;④S△AEF=
;④S△AEF= .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
相关试题

