【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
参考答案:
【答案】A
【解析】解:过点C作CD⊥x轴于D,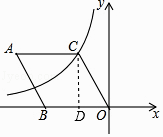
设菱形的边长为a,
在Rt△CDO中,OD=acos60°= ![]() a,CD=asin60°=
a,CD=asin60°= ![]() a,
a,
则C(﹣ ![]() a,
a, ![]() a),
a),
点A向下平移2个单位的点为(﹣ ![]() a﹣a,
a﹣a, ![]() a﹣2),即(﹣
a﹣2),即(﹣ ![]() a,
a, ![]() a﹣2),
a﹣2),
则 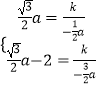 ,
,
解得 ![]() .
.
故反比例函数解析式为y=﹣ ![]() .
.
故选:A.
【考点精析】利用反比例函数的性质对题目进行判断即可得到答案,需要熟知性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料;
课堂上,老师设计了一个活动:将一个4×4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.
小方、小易和小红分别对网格进行了划分,结果如图①、图②、图③所示.
小方说:“我们三个人的划分方法都是正确的,但是将小红的整个图形(图③)逆时针旋转90
 后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”
后得到的划分方法与我的划分方法(图①)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同,”老师说:“小方说得对.”

完成下列问题:
(1)图④的划分方法是否正确?
(2)判断图⑤的划分方法与图②小易的划分方法是否相同,并说明你的理由.
(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图⑥中画出来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.
(1)求证:四边形CMPN是菱形;
(2)当P,A重合时,如图2,求MN的长;
(3)设△PQM的面积为S,求S的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
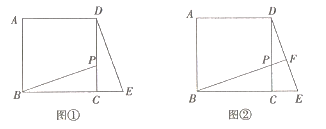
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b与反比例函数y=
 ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )
A.
B.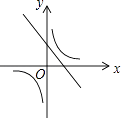
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在函数y1=﹣
 (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

相关试题

