搜索
【题目】如图，在△ABC中，∠B=32°，将△ABC沿直线m翻折，点B落在点D的位置，则∠1-∠2的度数是（ ）
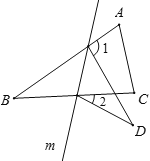
A. 32° B. 64° C. 65° D. 70°
参考答案：
【答案】B
【解析】
此题涉及的知识点是三角形的翻折问题，根据翻折后的图形相等关系，利用三角形全等的性质得到角的关系，然后利用等量代换思想就可以得到答案
如图，在△ABC中，∠B=32°，将△ABC沿直线m翻折，点B落在点D的位置
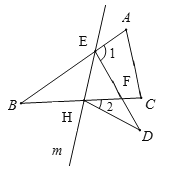
∠B=∠D=32° ∠BEH=∠DEH
∠1=180
-∠BEH-∠DEH=180-2∠DEH
∠2=180-∠D-∠DEH-∠EHF
=180-∠B-∠DEH-(∠B+∠BEH)
=180-∠B-∠DEH-（∠B+∠DEH）
=180-32°-∠DEH-32°-∠DEH
=180-64°-2∠DEH
∠1-∠2=180-2∠DEH-(180-64°-2∠DEH)
=180-2∠DEH-180+64°+2∠DEH
=64°
故选B
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
,点
分别在
直线上，点
为两平行线内部一点
（1）如图1，
角平分线交于点N，若
等于
，求
的度数（2）如图2，点G为直线
上一点，且
，延长GM交直线AB于点Q，点P为MG上一点，射线
相交于点H，满足
，设
，求
的度数（用
的代数式表示） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在6×6的正方形网格中，每个小正方形的边长为1，点A、B、C、D、E、F、M、N、P均为格点（格点是指每个小正方形的顶点）．
（1）利用图①中的网格，过P点画直线MN的平行线和垂线．
（2）把图②网格中的三条线段AB、CD、EF通过平移使之首尾顺次相接组成一个三角形（在图②中画出三角形）．
（3）第（2）小题中线段AB、CD、EF首尾顺次相接组成一个三角形的面积是______．
-
科目： 来源： 题型：
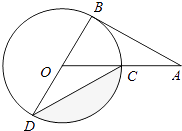
查看答案和解析>>【题目】如图，AB 为⊙O 的切线，切点为 B，连接 AO 与⊙O 交与点 C，BD 为⊙O 的直径，连接 CD，若∠A=30°，OA=2，则图中阴影部分的面积为（ ）
A.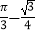
B.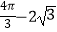
C.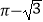
D.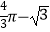
-
科目： 来源： 题型：
查看答案和解析>>【题目】周六上午，小亮去图书馆查资料，图书馆离家不远，他步行去图书馆，查完资料后他又边走边转去书店买书，在书店停留了几分钟后骑共享单车回家．"已知小亮离家的距离
(米)与离开家的时间
(分)之间的关系如图所示．请根据图象回答下列问题：（1）小亮出发几分钟后到达图书馆？
（2）小亮查完资料后步行的速度是多少？
（3）小亮
离开图书馆，几点回到家？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的一块地，∠ADC=90°，AD=4m，CD=3m，AB=13m，BC=12m，求这块地的面积．
相关试题
