【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图4所示.

(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
参考答案:
【答案】(1)初中部:平均数为85分,众数为85分;高中部:中位数为80分(2)中位数高的初中部成绩好些(3)初中代表队选手成绩较为稳定
【解析】试题分析:(1)根据平均数、众数、中位数的统计意义计算可补全统计表;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出初中、高中部的方差即可.
试题解析:(1)填表:初中平均数为:![]() (75+80+85+85+100)=85(分),
(75+80+85+85+100)=85(分),
众数85(分);高中部中位数80(分).
(2)初中部成绩好些.因为两个队的平均数都相同,初中部的中位数高,
所以在平均数相同的情况下中位数高的初中部成绩好些.
(3)∵![]() =
=![]() [(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70,
![]() =
=![]() [(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160.
[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160.
∴![]() <
<![]() ,因此,初中代表队选手成绩较为稳定.
,因此,初中代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(能简便的用简便方法计算)
(1)8+(-10)-(-5) (2)

(3)
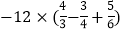 (4)
(4)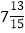 ×(-30)
×(-30)(5)
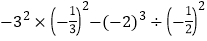
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2﹣
 x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0). 
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.

先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到
 ,
,整理,得
 .
. 所以
 .
.如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
整理,得 ,
所以 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调
彩电
进价(元/台)
5400
3500
售价(元/台)
6100
3900
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车厂计划半年内每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实每月生产量与计划量相比情况如下表(增加为正,减少为负)

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了,增加或减少多少?
相关试题

