搜索
【题目】已知：如图，线段AB＝10，C是AB的中点．
（1）求线段BC的长；
（2）若点D在直线AB上，DB＝2.5，求线段CD的长．
参考答案：
【答案】（1）BC =5；（2）线段CD的长为2.5或7.5．
【解析】试题分析: （1）根据线段中点的定义即可得到结论；
（2）如图1，点D在线段AB上，根据线段的和差求得结果；如图2，点D在线段AB的延长线上时，根据线段的和差求得结果．
试题解析:
解：（1）∵线段AB=10，C是AB的中点，∴BC=
AB=5；
（2）如图1，∵BC=5，BD=2.5，∴CD=BC﹣CD=2.5；
如图2，∵BC=5，BD=2.5，∴CD=BC+CD=7.5，
综上所述：线段CD的长为2.5或7.5．
点睛: 本题考查了两点间的距离，利用了线段中点的性质，线段的和差，分类讨论是解题关键，以防遗漏．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，A是数轴上表示－30的点，B是数轴上表示10的点，C是数轴上表示18的点，点A，B，C在数轴上同时向数轴的正方向运动，点A运动的速度是6个单位长度每秒，点B和C运动的速度是3个单位长度每秒．设三个点运动的时间为t秒(t≠5)，设线段OA的中点为P，线段OB的中点为M，线段OC的中点为N，当2PM－PN＝2时，t的值为_____．
-
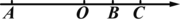
科目： 来源： 题型：
查看答案和解析>>【题目】【问题提出】已知∠AOB＝70°，∠AOD＝
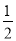∠AOC，∠BOD＝3∠BOC（∠BOC＜45°），求∠BOC的度数．【问题思考】聪明的小明用分类讨论的方法解决．
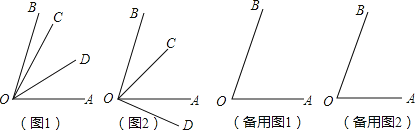
（1）当射线OC在∠AOB的内部时，①若射线OD在∠AOC内部，如图1，可求∠BOC的度数，解答过程如下：
设∠BOC＝α，∴∠BOD＝3∠BOC＝3α，∴∠COD＝∠BOD﹣∠BOC＝2α，∴∠AOD＝
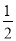∠AOC，∴∠AOD＝∠COD＝2α，∴∠AOB＝∠AOD+∠BOD＝2α+3α＝5α＝70°，∴α＝14°，∴∠BOC＝14°
问：当射线OC在∠AOB的内部时，②若射线OD在∠AOB外部，如图2，请你求出∠BOC的度数；
【问题延伸】（2）当射线OC在∠AOB的外部时，请你画出图形，并求∠BOC的度数．
【问题解决】综上所述：∠BOC的度数分别是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，AB是⊙O的一条弦，点C是优弧
上一点．（1）若∠ACB=45°，点P是⊙O上一点（不与A、B重合），则∠APB= ；
（2）如图②，若点P是弦AB与
所围成的弓形区域（不含弦AB与）内一点．求证：∠APB＞∠ACB；（3）请在图③中直接用阴影部分表示出在弦AB与
所围成的弓形区域内满足∠ACB＜∠APB＜2∠ACB的点P所在的范围．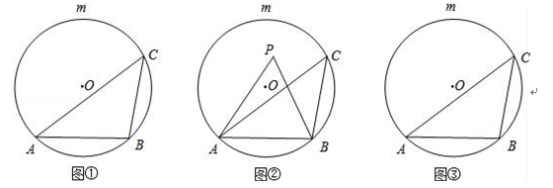
-
科目： 来源： 题型：
查看答案和解析>>【题目】用配方法解方程x2﹣8x+7＝0，配方后可得( )
A. (x﹣4)2＝9B. (x﹣4)2＝23
C. (x﹣4)2＝16D. (x+4)2＝9
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：-24x6y3÷=-4x2y2
-
科目： 来源： 题型：
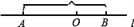
查看答案和解析>>【题目】如图，直线l上有AB两点，AB＝18cm，点O是线段AB上的一点，OA＝2OB
（1）OA＝＿＿＿＿＿cm， OB＝＿＿＿＿＿cm；
（2）若点C是直线AB上一点，且满足AC＝CO+CB，求CO的长；
（3）若动点P，Q分别从A，B同时出发，向右运动，点P的速度为3cm/s，点Q的速度为1cm/s．设运动时间为ts，当点P与点Q重合时，P，Q两点停止运动．
①当t为何值时，2OP﹣OQ＝4；
②当点P经过点O时，动点M从点O出发，以4cm/s的速度也向右运动．当点M追上点Q后立即返回，以4cm/s的速度向点P运动，遇到点P后再立即返回，以4cm/s的速度向点Q运动，如此往返.当点P与点Q重合时，P，Q两点停止运动．此时点M也停止运动．在此过程中，点M行驶的总路程是多少？
相关试题
