【题目】如图,两个可以自由转动的均匀转盘A、B,分别被分成4等分和3等分,并在每份内均标有数字.小花为甲、乙两人设计了一个游戏规则如下:同时自由转动转盘A、B;两个转盘停止后,(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),将两个指针所指份内的两个数字相乘,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜.但小强认为这样的规则是不公平的.
(1)请你用一种合适的方法(例如画树状图、列表)帮忙小强说明理由;
(2)请你设计一个公平的规则,并说明理由.

参考答案:
【答案】(1)甲获胜的机会大(2)公平的游戏规则不唯一
【解析】试题分析:(1)用列举法表示出所有可能的结果,根据所得结果分别计算积为偶数与积为奇数的概率,即可帮助小强说明理由;
(2)根据(1)中的结果制定公平的游戏规则即可(答案不唯一).
试题解析:(1)列表如下:
B A | 1 | 2 | 3 | 4 |
1 | 1×1=1 | 1×2=2 | 1×3=3 | 1×4=4 |
2 | 2×1=2 | 2×2=4 | 2×3=6 | 2×4=8 |
3 | 3×1=3 | 3×2=6 | 3×3=9 | 3×4=12 |
因为P(积为奇数)=![]() ,
,
P(积为偶数)=![]() ,
,
所以甲获胜的机会大;
(2)公平的游戏规则不唯一,例如:
如果自由转动两个转盘,转盘停止后,指针所指的两数之积为3的倍数时,甲获胜,否则乙获胜,
此时两人获胜的可能性均为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义一种新运算T,规定:T(x,y)=
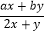 (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=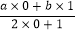 =b.
=b.(1)已知T(1,﹣1)=﹣2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组
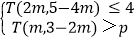 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,点B是数轴上在A点左侧的一点,且A、B两点间的距离为10,动点P从点A出发,以每秒3个单位长度的速度沿数轴向左运动.

(1)数轴上点B表示的数是 ;
(2)运动1秒时,点P表示的数是 ;
(3)动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?相遇时对应的有理数是多少?
②当点P运动多少秒时,点P与点Q的距离为8个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD沿对角线AC进行折叠,折叠后点D落在点F处,AF交BC于点E,有下列结论:①△ABF≌△CFB;②AE=CE;③BF∥AC;④BE=CE,其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图4所示.

(1)根据图示填写下表:
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,安排甲、乙两个工程队进行绿化.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在各自独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若绿化区域面积为1800m2,学校每天需付给甲队的绿化费用为0.4万元,每天需付给乙队的绿化费用为0.25万元,设安排甲队工作y天,绿化总费用为W万元.
①求W与y的函数关系式;
②要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件
 元的价格卖出这款童装,卖完后,这家商店( )
元的价格卖出这款童装,卖完后,这家商店( )A.盈利了B.亏损了
C.不赢不亏D.盈亏不能确定
相关试题

