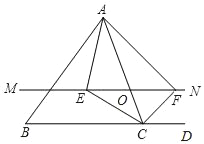
【题目】△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
参考答案:
【答案】略
【解析】
试题(1)由MN∥BC可得∠BCE=∠CEO,再结合∠BCE=∠ECO可得OE=OC,同理OC=OF,即可证得结论;
(2)先根据对角线互相平分的四边形的证得AECF为平行四边形,再根据CE、CF为△ABC内外角的平分线可得∠EOF=90°,即可证得结论.
(1)∵MN∥BC,
∴∠BCE=∠CEO
又∵∠BCE=∠ECO
∴∠OEC=∠OCE
∴OE=OC,同理OC=OF
∴OE=OF;
(2)当O为AC中点时,AECF为矩形
∵EO=OF,OA=OC
∴AECF为平行四边形
又∵CE、CF为△ABC内外角的平分线
∴∠EOF=90°,
∴AECF为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2
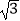 ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( ) 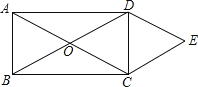
A.2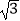
B.4
C.4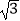
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
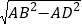 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
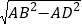 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
-
科目: 来源: 题型:
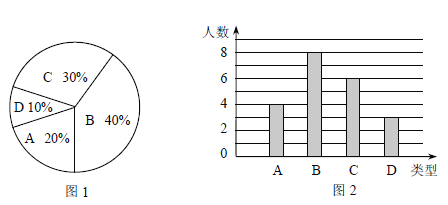
查看答案和解析>>【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:

① 小宇的分析是从哪一步开始出现错误的?
② 请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y=
 x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)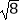 +(
+(  )﹣1﹣2cos45°﹣(π﹣2016)0
)﹣1﹣2cos45°﹣(π﹣2016)0
(2)2y2+4y=y+2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由.
(2)若∠B+∠C+∠BAC=180°,AD平分∠EAC,则AD∥BC吗?请说明理由.

相关试题

