【题目】现有一副直角三角板(角度分别为30°、60°、90°和45°、45°、90°),如图(1)所示,其中一块三角板的直角边AC垂直于数轴,AC的中点过数轴原点O,AC=8,斜边AB交数轴于点G,点G对应数轴上的数是4;另一块三角板的直角边AE交数轴于点F,斜边AD交数轴于点H.
(1)如果△AGH的面积是10,△AHF的面积是8,则点F对应的数轴上的数是 ,点H对应的数轴上的数是 ;
(2)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,若∠HAO=a,试用a来表示∠M的大小:(写出推理过程)
(3)如图(2),设∠AHF的平分线和∠AGH的平分线交于点M,设∠EFH的平分线和
∠FOC的平分线交于点N,求∠N+∠M的值.

参考答案:
【答案】(1)-5,-1(2)![]() ɑ+22.5°(3)∠M+∠N=97.5°.
ɑ+22.5°(3)∠M+∠N=97.5°.
【解析】(1)-5,-1
(2) ∵∠AHF的平分线和∠AGH的平分线交于点M,
∴∠FHM=![]() ∠FHA,∠HGM=
∠FHA,∠HGM=![]() ∠HGA,
∠HGA,
∵∠FHM=∠M+∠HGM,∠FHA=∠HGA+∠HAG,
∴2∠M+2∠HGM=∠HGA+∠HAG,
∴∠M=![]() ∠HAG=
∠HAG=![]() (∠HAO+∠OAG)=
(∠HAO+∠OAG)=![]() ɑ+22.5°
ɑ+22.5°
(3) ∵∠EFH的平分线和∠FOC的平分线交于点N,
∴∠N=90°-![]() ∠FAO=90°-
∠FAO=90°-![]() ∠FAH-
∠FAH-![]() ∠OAH (可以直接利用∠N=90°-
∠OAH (可以直接利用∠N=90°-![]() ∠FAO)
∠FAO)
=90°-15°-![]() ∠OAH
∠OAH
=75°-![]() ∠OAH,
∠OAH,
∵∠M=![]() ∠OAH+22.5°,
∠OAH+22.5°,
∴∠M+∠N=97.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入,因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系.在这种情况下,如果要保证每周
 万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元? 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
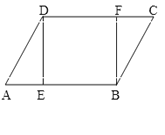
(1)求证:
 ≌
≌ .
.(2)若
 DEB=90
DEB=90 ,求证四边形DEBF是矩形.
,求证四边形DEBF是矩形. -
科目: 来源: 题型:
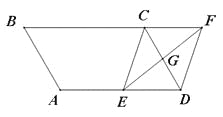
查看答案和解析>>【题目】(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.

(1)图②有_____个三角形;图③有_____个三角形.
(2)按上面的方法继续下去,第
 个图形中有 个三角形?
个图形中有 个三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】作图,思考并回答问题:如图,已知:ABC
(1)按下列要求作图:取边AB、AC的中点D、E,连结线段DE;
(2)用刻度尺测量线段 DE、BC的长度分别为 ;
(3)用量角器得
 B与
B与 ADE的度数分别为 ;
ADE的度数分别为 ;(4)通过(2)、(3)你发现DE与BC什么关系?请写出你的猜想.

相关试题

