【题目】探究题:如图,在等腰三角形ABC中,AB=AC,其底边长为8 cm,腰长为5 cm,一动点P在底边上从点B出发向点C以0.25 cm/s的速度移动,请你探究:当点P运动多长时间时,点P与顶点A的连线PA与腰垂直.

参考答案:
【答案】当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
【解析】
利用勾股定理求出AD的长,再利用勾股定理逆定理即可证明垂直.
(1)过点A作AD⊥BC于点D.

∵AB=AC,BC=8 cm,
∴BD=CD=![]() BC=4 cm.
BC=4 cm.
由勾股定理,得AD=![]() =3(cm).
=3(cm).
分两种情况:(1)如图,当点P运动t秒后有PA⊥AC(P在线段BD上)时,
∵AP2=PD2+AD2=PC2-AC2,
∴PD2+32=(PD+4)2-52,∴PD=2.25 cm,
∴BP=4-2.25=1.75,
∴0.25t=1.75,解得t=7.
(2)当点P运动t秒后有PA⊥AB(P在线段CD上)时,同理可得PD=2.25,∴BP=4+2.25=6.25,
∴0.25t=6.25,解得t=25.
综上所述,当点P运动的时间为7 s或25 s时,点P与顶点A的连线与腰垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )
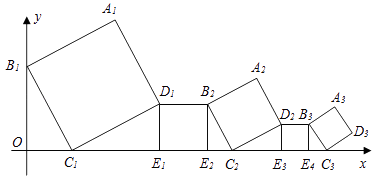
A.( )2016
)2016
B.( )2017
)2017
C.(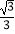 )2016
)2016
D.(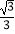 )2017
)2017 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C三点在同一条直线上.
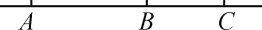
(1)用上述字母表示的不同线段共有____条,它们是______________________;
(2)用上述字母表示的不同射线共有____条,它们是______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示3,点B表示-
 .
.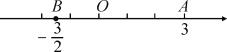
(1)数轴是什么图形?
(2)数轴上原点O左边的部分(包括原点)是什么图形?怎样表示?
(3)射线OB上的点表示什么数?端点表示什么数?
(4)数轴上表示不小于-
 且不大于3的部分是什么图形?怎样表示?
且不大于3的部分是什么图形?怎样表示?
相关试题

