【题目】在边长为![]() 的等边三角形
的等边三角形![]() 中,
中,![]() 是
是![]() 边上任意一点,过点
边上任意一点,过点![]() 分别作
分别作![]() ,
,![]() ,
,![]() 、
、![]() 分别为垂足.
分别为垂足.
(1)求证:不论点![]() 在
在![]() 边的何处时都有
边的何处时都有![]() 的长恰好等于三角形
的长恰好等于三角形![]() 一边上的高;
一边上的高;
(2)当![]() 的长为何值时,四边形
的长为何值时,四边形![]() 的面积最大,并求出最大值.
的面积最大,并求出最大值.
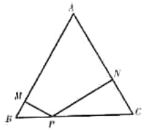
参考答案:
【答案】(1)PM+PN=CD;(2)1,![]() .
.
【解析】
试题分析:(1)连接AP,过C作CD⊥AB于D,根据等边三角形的性质得到AB=AC,根据三角形的面积公式列方程即可得到结论;
(2)设BP=x,则CP=2﹣x,由△ABC是等边三角形,得到∠B=∠C=60°,解直角三角形得到BM=![]() x,PM=
x,PM=![]() x,CN=
x,CN=![]() (2﹣x),PN=
(2﹣x),PN=![]() (2﹣x),根据二次函数的性质即可得到结论.
(2﹣x),根据二次函数的性质即可得到结论.
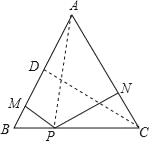
试题解析:(1)连接AP,过C作CD⊥AB于D,
∵△ABC是等边三角形,
∴AB=AC,
∵S△ABC=S△ABP+S△ACP,
∴![]() AB·CD=
AB·CD=![]() AB·PM+
AB·PM+![]() AC·PN,
AC·PN,
∴PM+PN=CD,
即不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高;
(2)设BP=x,则CP=2﹣x,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵PM⊥AB,PN⊥AC,
∴BM=![]() x,PM=
x,PM=![]() x,CN=
x,CN=![]() (2﹣x),PN=
(2﹣x),PN=![]() (2﹣x),
(2﹣x),
∴四边形AMPN的面积=![]() ×(2﹣
×(2﹣![]() x)
x)![]() x+
x+![]() [2﹣
[2﹣![]() (2﹣x)]·
(2﹣x)]·![]() (2﹣x)=
(2﹣x)=![]() ,
,
∴当BP=1时,四边形AMPN的面积最大,最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(﹣3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
(1)求这两个函数的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求三角形AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种细菌的直径是0.0000005厘米,用科学记数法表示为厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】气候宜人的省级度假胜地吴川吉兆,测得一至五月份的平均气温分别为17、17、20、22、24(单位:℃),这组数据的中位数是( )
A.24
B.22
C.20
D.17 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2﹣2ab+b2﹣c2= . y2﹣7y+12= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 关于某直线对称的两个图形一定能够重合
B. 长方形是轴对称图形
C. 两个全等的三角形一定关于某直线对称
D. 轴对称图形的对称轴至少有一条
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个小正方形边长都为1个单位长度.

①画出将△ABC向下平移4个单位得到的△A1B1C1;
②画出△ABC关于原点O的中心对称图形△A2B2C2;
③画出△A1B1C1绕着点A1顺时针方向旋转90°后得到的△A3B3C3 .
相关试题

