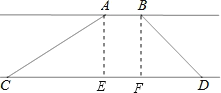
【题目】如图,两条互相平行的河岸,在河岸一边测得AB为20米,在另一边测得CD为70米,用测角器测得∠ACD=30°,测得∠BDC=45°,求两条河岸之间的距离.(![]() ,
, ![]() ≈1.7,结果保留整数)
≈1.7,结果保留整数)

参考答案:
【答案】两条河岸之间的距离约为18米.
【解析】试题分析:分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h.则AE=BF=h,EF=AB=20.解Rt△ACE,得出CE=![]() h,解Rt△BDF,求出DF=BF=h,根据CD=CE+EF+FD=70列出方程,求解即可.
h,解Rt△BDF,求出DF=BF=h,根据CD=CE+EF+FD=70列出方程,求解即可.
试题解析:如图,分别过点A、B作CD的垂线交CD于点E、F,令两条河岸之间的距离为h.
∵AE⊥CD,BF⊥CD,AB∥CD,AB=20,
∴AE=BF=h,EF=AB=20.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴tan∠ACE=![]() ,即tan30°=
,即tan30°=![]() ,
,
∴CE=![]() h.
h.
在Rt△BDF中,∵∠BFD=90°,∠BDF=45°,
∴DF=BF=h.
∵CD=70,
∴CE+EF+FD=70,
∴![]() h+20+h=70,
h+20+h=70,
∴h=25(![]() ﹣1)≈18.
﹣1)≈18.
答:两条河岸之间的距离约为18米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二元一次方程2x+y—3=0化成用x表示y的形式,则y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】木工师傅在锯木料时,一般先在木料上画出两个点,然后过这两个点弹出一条墨线,这是因为_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A在第三象限,到x轴的距离为3,到y轴的距离为4,则点A的坐标为( )
A. (3,4) B. (﹣3,4) C. (﹣4,﹣3) D. (﹣3,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=
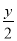 ,把x=
,把x= ,代入已知方程,
,代入已知方程,得(
 )2 +
)2 + ﹣1=0.
﹣1=0.化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
相关试题

