【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度的速度向点
方向以每秒2个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒1个单位长度的速度向点
方向以每秒1个单位长度的速度向点![]() 匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒
秒![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?若能,求出
能够成为菱形吗?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(3)当![]() ________时,
________时,![]() 为直角三角形.
为直角三角形.
参考答案:
【答案】(1)详见解析;(2)能;(3)2或![]() 秒
秒
【解析】
(1)在中![]() ,
,![]() ,
,![]() ,由已知条件求证;
,由已知条件求证;
(2)求得四边形![]() 为平行四边形,若使平行四边形
为平行四边形,若使平行四边形![]() 为菱形则需要满足的条件及求得;
为菱形则需要满足的条件及求得;
(3)分三种情况:①![]() 时,四边形
时,四边形![]() 为矩形.在直角三角形
为矩形.在直角三角形![]() 中求得
中求得![]() 即求得.②
即求得.②![]() 时,由(2)知
时,由(2)知![]() ,则得
,则得![]() ,求得
,求得![]() .③
.③![]() 时,此种情况不存在.
时,此种情况不存在.
(1)在![]() 中,
中,![]()
![]()
∴![]()
又∵![]()
∴![]()
(2)能. 理由如下:
∵![]() ,
,![]()
∴![]()
又∵![]()
∴四边形![]() 为平行四边形
为平行四边形
在![]() 中,
中,![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,
,![]()
∴![]()
当![]() 时,
时,![]() 为菱形
为菱形
∴AD=![]()
∴![]() ,即
,即![]() 秒时,四边形
秒时,四边形![]() 为菱形
为菱形
(3)①![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
②![]() 时,由(2)四边形
时,由(2)四边形![]() 为平行四边形知
为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
则有![]() ,
,![]() .
.
③当![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或
秒或![]() 秒时,
秒时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
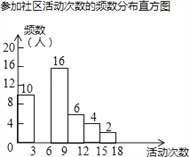
参加社区活动次数的频数、频率分布表
活动次数x
频数
频率
0<x≤3
10
0.20
3<x≤6
a
0.24
6<x≤9
16
0.32
9<x≤12
6
0.12
12<x≤15
m
b
15<x≤18
2
n
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=
 ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)= .
.(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
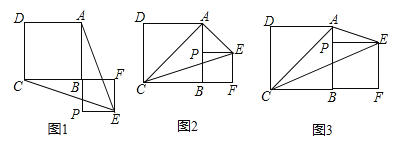
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B是反比例函数y=
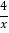 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )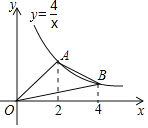
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
(1)求c1的解析式;
(2)若直线l1:y=x+m与c1仅有唯一的交点,求m的值;
(3)若抛物线c1关于y轴对称的抛物线记作c2,平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;
(4)若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.

相关试题

