【题目】AD是△ABC的边BC上的中线，AB=12，AC=8，则边BC的取值范围是 ；中线AD的取值范围是 ．

参考答案：

【答案】4＜BC＜20，2＜AD＜10．

【解析】

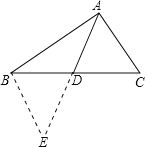
试题分析：BC边的取值范围可在△ABC中利用三角形的三边关系进行求解，而对于中线AD的取值范围可延长AD至点E，使AD=DE，得出△ACD≌△EBD，进而在△ABE中利用三角形三边关系求解．

解：如图所示，

在△ABC中，则AB﹣AC＜BC＜AB+AC，

即12﹣8＜BC＜12+8，4＜BC＜20，

延长AD至点E，使AD=DE，连接BE，

∵AD是△ABC的边BC上的中线，∴BD=CD，

又∠ADC=∠BDE，AD=DE

∴△ACD≌△EBD，∴BE=AC，

在△ABE中，AB﹣BE＜AE＜AB+BE，即AB﹣AC＜AE＜AB+AC，

12﹣8＜AE＜12+8，即4＜AE＜20，

∴2＜AD＜10．

故此题的答案为4＜BC＜20，2＜AD＜10．

关闭