【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= ![]() ACBD,其中正确的结论有( )
ACBD,其中正确的结论有( ) 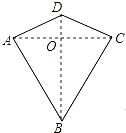
A.0个
B.1个
C.2个
D.3个
参考答案:
【答案】D
【解析】解:在△ABD与△CBD中, 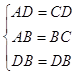 ,
,
∴△ABD≌△CBD(SSS),
故①正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,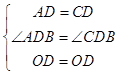 ,
,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故②正确;
四边形ABCD的面积= ![]() =
= ![]() ACBD,
ACBD,
故③正确;
故选D.
先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值相等的两个数在数轴上对应的两点距离为8,则这两个数为( )
A.+8或﹣8
B.+4或﹣4
C.﹣4或+8
D.﹣8或+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示:试化简:|a+b|﹣|b|﹣|a﹣c|﹣|1﹣c|

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3+(﹣2)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD所在直线是△ABC的对称轴,点E、F是AD上的两点,若BC=4,AD=3,则图中阴影部分的面积的值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣24﹣(﹣4)2×(﹣1)+(﹣3)2;
-
科目: 来源: 题型:
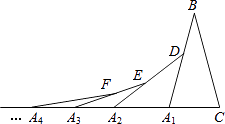
查看答案和解析>>【题目】如图,在第一个△A1BC中,∠B=30°,A1B=CB,在边A1B上任取一D,延长CA2到A2 , 使A1A2=A1D,得到第2个△A1A2D,在边A2B上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第三个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是度.
相关试题

