【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.

参考答案:
【答案】(1)证明见解析; (2)证明见解析.
【解析】
(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明.
解:(1)延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,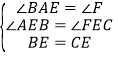 ,
,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAD的平分线,
∴∠BAE=∠EAD,
∵AB∥CD,
∴∠BAE=∠F,
∴∠EAD=∠F,
∴AD=DF,
∴AD=DF=DC+CF=DC+AB,
(2)如图②,延长AE交DF的延长线于点G,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G,
在△AEB和△GEC中, 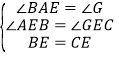 ,
,
∴△AEB≌△GEC,
∴AB=GC,
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG,
∵AB∥CD,
∴∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∴AB=CG=AF+CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红家有一块L形的菜地,要把L形的菜地按如图所示分成两块面积相等的梯形,种上不同的蔬菜.这两个梯形的上底都是a m,下底都是b m,高都是(b-a) m.
(1)求小红家这块L形菜地的面积.(用含a、b的代数式表示)
(2)若a2+b2=15,ab=5,求小红家这块L形菜地的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=
 ,下列说法错误的是( )
,下列说法错误的是( )
A.这个函数的图象位于第一、第三象限
B.这个函数的图象既是轴对称图形又是中心对称图形
C.当x>0时,y随x的增大而增大
D.当x<0时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
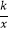 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
A.(﹣6,1)
B.(1,6)
C.(2,﹣3)
D.(3,﹣2) -
科目: 来源: 题型:
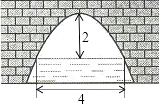
查看答案和解析>>【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
A.3
B.2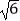
C.3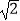
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点M(﹣3,2)分别作x轴、y轴的垂线与反比例函数y=
 的图象交于A,B两点,则四边形MAOB的面积为 .
的图象交于A,B两点,则四边形MAOB的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读题.
材料一:若一个整数m能表示成a2-b2(a,b为整数)的形式,则称这个数为“完美数”.例如,3=22-12,9=32-02,12=42-22,则3,9,12都是“完美数”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整数),所以M也是”完美数”.
材料二:任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=
 .例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)= .请解答下列问题:
.请解答下列问题:(1)8______(填写“是”或“不是”)一个完美数,F(8)= ______.
(2)如果m和n都是”完美数”,试说明mn也是完美数”.
(3)若一个两位数n的十位数和个位数分别为x,y(1≤x≤9),n为“完美数”且x+y能够被8整除,求F(n)的最大值.
相关试题

