【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为BC边的中点,过点B作BF⊥AB交AD的延长线于点F,CE平分∠ACB交AD于点E.
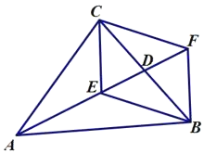
(1)判断四边形CEBF的形状,并证明;
(2)若AD=![]() ,求BF及四边形CEBF的面积.
,求BF及四边形CEBF的面积.
参考答案:
【答案】(1)四边形CEBF是平行四边形,证明见解析;(2)![]() ,四边形CEBF的面积=12.
,四边形CEBF的面积=12.
【解析】
(1)由等腰直角三角形的性质、垂直的定义和角平分线的定义可得∠DCE=∠CBF,而可根据ASA证明△CDE≌△BDF,于是可得DE=DF,进一步即可得出结论;
(2)设CD=x,则AC=BC=2x,然后在Rt△ACD中,由勾股定理可求出x,从而可得AC、AB的长,由等腰三角形的性质可得CE垂直平分AB,进而可得AE=BE,然后根据等腰三角形的性质和判定以及余角的性质可得AE=EF,于是可得AD=3DE,AF=4DE,而AD已知,则DE和AF可得,于是可在直角△AFB中根据勾股定理求出BF,过点C作CG⊥DE于点G,如图,则由三角形的面积可求出CG的长,于是可得△CDE的面积,而所求的四边形CEBF的面积是△CDE面积的4倍,问题即得解决.
(1)四边形CEBF是平行四边形.
证明:∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵FB⊥AB,
∴∠ABF=90°,
∴∠CBF=45°,
∵CE平分∠ACB,
∴∠DCE=45°=∠CBF,
又∵DC=DB,∠CDE=∠BDF,
∴△CDE≌△BDF(ASA),
∴DE=DF,
∵DC=DB,
∴四边形CEBF是平行四边形;
(2)解:设CD=x,则AC=BC=2x,
在Rt△ACD中,由勾股定理得:![]() ,
,
解得:x=3,
∴CD=3,AC=BC=6,
∴![]() ,
,
∵AC=BC,CE平分∠ACB,
∴CE垂直平分AB,
∴AE=BE,
∴∠BAE=∠ABE,

∵∠BAE+∠AFB=90°,∠ABE+∠FBE=90°,
∴∠AFB=∠FBE,
∴EF=BE,
∴AE=EF,
∵EF=2DE,
∴AD=3DE,AF=4DE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
过点C作CG⊥DE于点G,如图,则由三角形的面积可得:![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
∴S△CDE =![]() ,
,
∴四边形CEBF的面积=4S△CDE=4×3=12.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为w元,当每间房价定价为多少元时,宾馆每天所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(+3.41)(0.59)
(2)(13
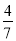 )(13
)(13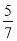 )
)(3)20+(14)(18)13
(4)(+3)(21)+(19)+(+12)+(+5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为
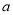 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了帮助湖北省武汉市防控新冠肺炎,某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物资共2000件送往灾区,已知每件甲种物资的价格比每件乙种物资的价格贵10元,用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同.
(1)求甲、乙两种救灾物资每件的价格各是多少元?
(2)经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,若该爱心组织如何购买这2000件物资,才能使得购买资金最少?
相关试题

