【题目】某经销商销售一种圆盘,圆盘的半径x(cm),圆盘的售价y与x成正比例,圆盘的进价与x2成正比例,售出一个圆盘的利润是P(元).当x=10时,y=80,p=30.(利润=售价﹣进价).
(1)求y与x满足的函数关系式;
(2)求P与x满足的函数关系式;
(3)当售出一个圆盘所获得的利润是32元时,求这个圆盘的半径.
参考答案:
【答案】
(1)
解:由题意得,y=kx(k≠0),
∵x=10时,y=80,
∴10k=80,k=8.
∴y与x满足的函数关系式为y=8x
(2)
解:由题意,设进价为mx2,则P=y﹣mx2=﹣mx2+8x.
∵当x=10时,P=30,
∴30=﹣m102+8×10,
∴m= ![]() .
.
∴P与x满足的函数关系式为P=﹣ ![]() x2+8x
x2+8x
(3)
解:由题意得,﹣ ![]() x2+8x=32,
x2+8x=32,
化简得,x2﹣16x+64=0,
解得x1=8;x2=﹣8(舍).
则这个圆盘的半径是8cm
【解析】(1)根据“圆盘的售价y与x成正比例”可设y=kx(k≠0),再根据x=10时,y=80,利用待定系数法求出k,可得y与x满足的函数关系式;(2)根据题意可设进价为mx2 , 则P=y﹣mx2=﹣mx2+8x,然后再把x=10时,P=30代入即可算出m的值,进而得到P与x满足的函数关系式;(3)把P=32代入(2)中的解析式,计算即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1和2,四边形ABCD是菱形,点P是对角线AC上一点,以点P为圆心,PB为半径的弧,交BC的延长线于点F,连接PF,PD,PB.

(1)如图1,点P是AC的中点,请写出PF和PD的数量关系:;
(2)如图2,点P不是AC的中点,
①求证:PF=PD.
②若∠ABC=40°,直接写出∠DPF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC各顶点的坐标分A(-2,-2),B(-4,-1),C(-4,-4).

(1)作出△ABC关于原点O成中心对称的△A1B1C1;
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在
△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了扩大经营,决定购进6台机器用于生产某种活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元.
甲
乙
价格(万元/台)
7
5
每台日产量(个)
100
60
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D是 AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,BC=AC=5,AB=8,CD为AB边上的高,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面上滑动.如图2,设运动时间表为t秒,当B到达原点时停止运动.
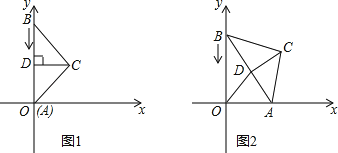
(1)当t=0时,求点C的坐标;
(2)当t=4时,求OD的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点D运动路线的长;
(4)当以点C为圆心,CA为半径的圆与坐标轴相切时,求t的值.
相关试题

