【题目】如图,正方形ABCD的边长为4+2![]() , 点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是 .
, 点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是 .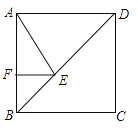
参考答案:
【答案】2
【解析】解:设EF=x,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,∠ABD=∠ADB=45°,
∴BD=![]() AB=4
AB=4![]() +4,EF=BF=x,
+4,EF=BF=x,
∴BE=![]() x,
x,
∵∠BAE=22.5°,
∴∠DAE=90°﹣22.5°=67.5°,
∴∠AED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠DAE,
∴AD=ED,
∴BD=BE+ED=![]() x+4+2
x+4+2![]() =4
=4![]() +4,
+4,
解得:x=2,
即EF=2;
所以答案是:2.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长是4,对角线AC、BD交于点O,点E在线段AC上,且OE=
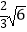 , 则∠ABE的度数 度.
, 则∠ABE的度数 度. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣8= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(
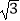 , 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .
, 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .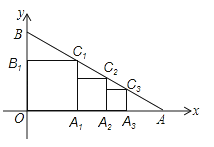
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(1)(3a2-8a)+(2a2-13a2+2a)-2(a3-3),其中a=-2;
(2)3x2y-
 +3xy2,其中x=3,y=-
+3xy2,其中x=3,y=- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为3和5的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则ET的长为
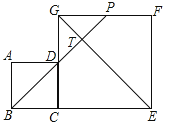
-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上书写了一个正确的验算过程,随后用手掌捂住了一个二次三项式,形式如下:
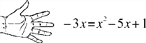
(1)求所捂的二次三项式;
(2)若-x2+2x=1,求所捂二次三项式的值.
相关试题

