Question

【题目】阅读下列材料，然后解决问题：

截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．

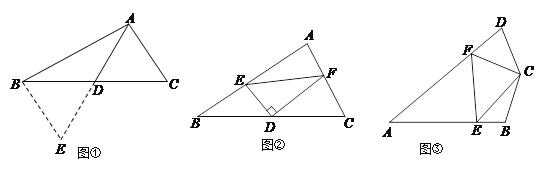
(1)如图①，在△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是 ；

(2)问题解决：

如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE＋CF＞EF；

(3)问题拓展：

如图③，在四边形ABCD中，∠B＋∠D＝180°，CB＝CD，∠BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

Answer 1

【答案】(1) (2)证明见解析(3)BE＋DF＝EF

【解析】试题分析：（1）延长AD至E，使DE=AD，连接BE．由SAS证明△BDE≌△CDA，得出BE=AC=6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；

（2）延长FD至点G，使DG＝DF，连接BG，EG．同（1）得△BDG≌△CDF，得出BG＝CF，由线段垂直平分线的性质得出EF＝EG，在△BEG中，由三角形的三边关系得出BE＋BG>EG即可得出结论；

（3）延长AB至点G，使BG=DF，连接CG．证出∠CBG＝∠D，由SAS证明△CBG≌△CDF，得出CG＝CF，∠BCG＝∠DCF，证出∠ECG=70°=∠ECF，再由SAS证明△ECG≌△ECF，得出EG=EF，即可得出结论．

解：（1）延长AD至E，使DE=AD，连接BE，如图①所示：

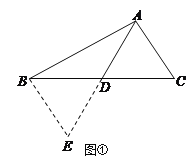
∵AD是BC边上的中线，∴BD=CD，在△BDE和△CDA中，∵BD=CD，∠BDE=∠CDA，DE=AD，∴△BDE≌△CDA（SAS），∴BE=AC=6，在△ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，∴12﹣8＜AE＜12+8，即4＜AE＜20，∴2＜AD＜10；

(2)证明：延长FD至点G，使DG＝DF，连接BG，EG．

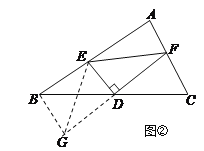
∵点D是BC的中点，∴DB＝DC．

在△BDG和△CDF中，

∵DG=DF，∠BDG=∠CDF，DB=DC，∴△BDG≌△CDF(SAS)，∴BG＝CF．

∵ED⊥FD，即ED⊥FG．

又∵FD＝GD，∴EF＝EG．

在△BEG中，∵BE＋BG>EG， ∴BE＋CF>EF．

(3)解：BE＋DF＝EF．证明如下：

如图，延长AB至点G，使BG＝DF，连接CG．

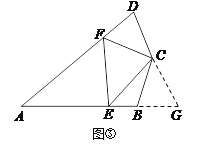
∵∠ABC＋∠D＝180°，∠ABC＋∠CBG＝180°，∴∠CBG＝∠D．

在△CBG和△CDF中，

∵BG=DF，∠CBG=∠CDF，CB=CD，∴△CBG≌△CDF(SAS)， ∴CG＝CF，∠BCG＝∠DCF，．

∵∠BCD＝140°，∠ECF＝70°，∴∠DCF＋∠BCE＝70°，∴∠BCE＋∠BCG＝70°，∴∠ECG＝∠ECF＝70°．

在△ECG和△ECF中，

∵CE=CE，∠ECG=∠ECF，CG=C，∴△ECG≌△ECF(SAS)，∴EG＝EF．

∵BE＋BG＝EG，∴BE＋DF＝EF．