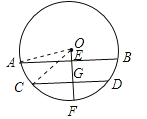
【题目】如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深GF=2cm.若水面上升2cm(EG=2cm),则此时水面宽
AB为多少?

参考答案:
【答案】![]() cm.
cm.
【解析】试题分析:连接OA、OC.设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.根据垂径定理,得CG=10.在直角三角形OCG中,根据勾股定理求得R的值,再进一步在直角三角形OAE中,根据勾股定理求得AE的长,从而再根据垂径定理即可求得AB的长.
试题解析:解:如图所示,连接OA、OC.
设⊙O的半径是R,则OG=R﹣2,OE=R﹣4.
∵OF⊥CD,∴CG=![]() CD=10cm.
CD=10cm.
在直角三角形COG中,根据勾股定理,得
R2=102+(R﹣2)2,解,得R=26.
在直角三角形AOE中,根据勾股定理,得
AE=![]() =
=![]() cm.
cm.
根据垂径定理,得AB=![]() (cm).
(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG,AH=CF.

(1)求证:四边形EFGH是平行四边形;
(2)如果AB=AD,且AH=AE,求证:四边形EFGH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,﹣6),则A点的对应点A′坐标为( )
A. (﹣2,﹣4) B. (﹣4,﹣2) C. (﹣1,﹣4) D. (1,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
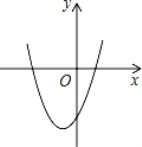
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
相关试题

