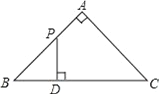
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. 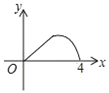 B.
B. 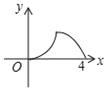 C.
C. 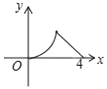 D.
D. 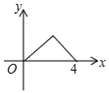
参考答案:
【答案】B
【解析】过A点作AH⊥BC于H,利用等腰直角三角形的性质得到∠B=∠C=45°,BH=CH=AH=![]() BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=
BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=![]() x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣
x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣![]() x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH=![]() BC=2,
BC=2,
当0≤x≤2时,如图1,
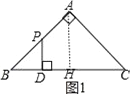
∵∠B=45°,
∴PD=BD=x,
∴y=![]() xx=
xx=![]() x2;
x2;
当2<x≤4时,如图2,
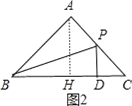
∵∠C=45°,
∴PD=CD=4﹣x,
∴y=![]() (4﹣x)x=﹣
(4﹣x)x=﹣![]() x2+2x,
x2+2x,
故选B
“点睛”本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力,解决本题的关键是利用分类讨论的思想求出y与x的函数关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在西部大开发中,为了改善生态环境,鄂西政府决定绿化荒地,计划第1年先植树1.5万亩,以后每年比上一年增加1万亩,结果植树总数是时间(年)的一次函数,则这个一次函数的图象是( )
A.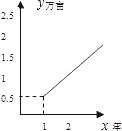
B.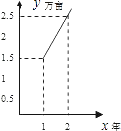
C.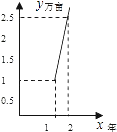
D.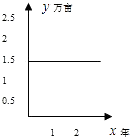
-
科目: 来源: 题型:
查看答案和解析>>【题目】从A地向B地打长途,不超3分钟,收费2.4元,以后每超一分超加收一元,若通话时间为t分钟(t≥3且t是整数),则付话费y元与t分钟函数关系式是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,且△ABC与△A′B′C′的相似比为1:2,则△ABC与△A′B′C′的面积比是( )
A.1:1
B.1:2
C.1:3
D.1:4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+2a﹣3=0,则代数式2a2+4a﹣3的值是( )
A.﹣3
B.0
C.3
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
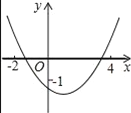
A. c>﹣1 B. b>0 C. 2a+b≠0 D. 9a+c>3b
-
科目: 来源: 题型:
查看答案和解析>>【题目】张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2.S1与t之间的函数关系如图所示,请你解答下列问题:
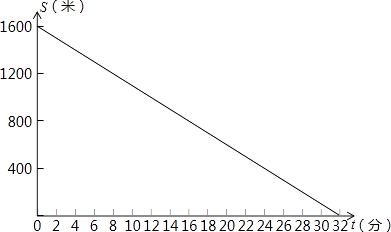
(1)李老师步行的速度为
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
相关试题

